
ITエンジニアのための機械学習理論入門
第 7 章 EM アルゴリズム:最尤推定法による教師なし学習
こんにちは。クラウドエースのエンジニアの神谷です。
この記事は、Google Cloud 中井悦司さんの著書「IT エンジニアのための機械学習理論入門」の内容を参考に、機械学習の裏にある数学的な理論をわかりやすく紹介していきます。

昨今では、機械学習という技術がますます一般化されていますが、その分触れる事が少なくなった理論部分が、中井さんの書籍ではとてもわかりやすく解説されています。
ここでは特に重要と思われるポイントを、章ごとに記事としてまとめています。
「このような内容をもっと詳しく勉強したい!」と感じた方は、これらの記事を参考にしながら、中井さんの書籍を読んでいただければ、より深く掘り下げて理解を深めることができるでしょう。
本章の位置づけ
本章では、「最尤推定法(3 章参照)」を用いた教師なし学習「EM アルゴリズム」について説明します。題材として MNIST の手書き数字画像を取り上げ、EM アルゴリズムを用いて、数字画像のクラスタリング・生成をおこないます。また、k 平均法(6章参照)との類似点についても述べます。
EM アルゴリズムとは
EM アルゴリズム は、「Expectation–Maximization algorithm」の略であり、確率モデルのパラメータを最尤推定する手法の一つです。観測不可能な潜在変数に確率モデルが依存するケースで最尤推定法を適用するために用います。
例えば、本記事のように正解ラベルを持たない文字データを扱う場合、各文字がどれぐらい発生するかどうかは観測不可能です。こういった状況の中で、どのように EM アルゴリズムが使えるのかを見ていきます。
この観測不可能な潜在変数のことを「隠れ変数」と言います。
EM アルゴリズムは反復法(数値解析分野における手法のうち、反復計算を用いるものの総称)の一種であり、期待値(E:Expectation)ステップと最大化(M:Maximization)ステップを交互に繰り返します。
① E(Expectation)ステップは「隠れ変数」に関する期待値を取る操作であり、確率モデルのパラメータを固定して、計算式に従って「隠れ変数の事後確率」を求めます。これは、モデルの尤度の期待値に相当します。
② M(Maximization)ステップでは、E ステップで求めた「隠れ変数の事後確率(≒ モデルの尤度の期待値)」を最大化するようなパラメータを求めます。
③反復ステップでは、M ステップで求まったパラメータは次の E ステップで使われる「隠れ変数」の分布を決定するために用いられます。
また、EM アルゴリズム は、混合正規分布のような「ソフト・クラスタリング」に用いる手法であり、6 章で説明した「k 平均法」に代表される「ハード・クラスタリング」とは以下の点で異なります。
- ハード・クラスタリング: 一つのデータは一つのクラスタにのみ分類される。
- ソフト・クラスタリング: 一つのデータは複数のクラスタに確率的に分類される。データ分布に確率モデルをあてはめ、どのクラスタに属するかを確率的に決める。
3. ベルヌーイ分布を用いた最尤推定法
手書き数字の画像を EM アルゴリズムで分類・生成する前に、まずは要素を一つずつ確認していきましょう。最終的には、「特定の数字のクラスタごとに画像生成を行う」というモデルを作成しますが、まずは、簡単に特定の数字だけの場合を考えます。
次のような数字のデータ(以下の ”0”〜”9” の手書き数字画像)から、「画像生成器」を作成します。ここでは、”3″ のみを用いるものとします。

「画像生成器」を作成するにあたり、「画像生成器」から与えられたデータが生成される確率(尤度)を最大化するという条件を適用します。すると、このあと説明するようにこの「画像生成器」は、各画像の平均を取った「代表画像」と一致することがわかります。
まずは「代表画像」を理解し、「画像生成器」といった本章の前提となる重要な概念について説明していきます。
代表画像
まず「代表画像」について説明します。
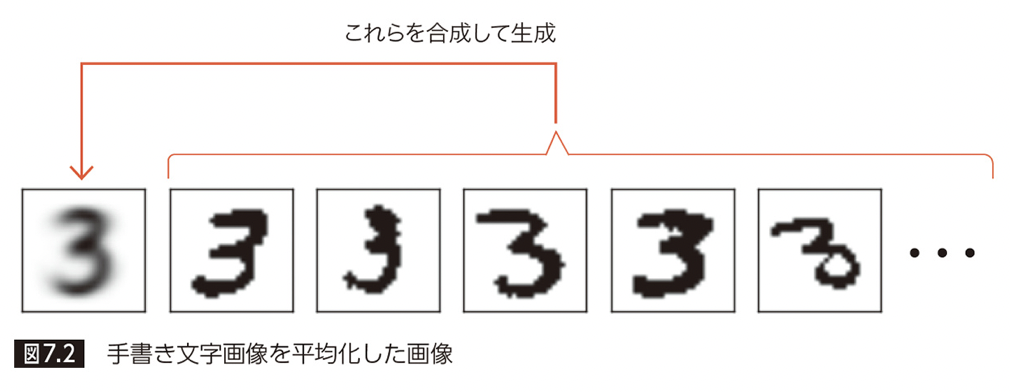
と言っても、代表画像の定義は非常にシンプルで、与えられた複数の画像を平均化したものです。次の図で、左から 2 番目以降の画像群の各ピクセルの平均をとったものが、代表画像(一番左の画像)になります。
MNIST 手書き画像の具体的なピクセル値を図示すると、下図のようになります。
(MNIST 画像は、ピクセル値が 0 ~ 255 のグレースケール画像ですが、ここでは 0,1 に二値化しています。また値域の反転も行っています。)

ここで、例えば 3 つの手書き数字画像から平均画像を生成すると、次のようになります。
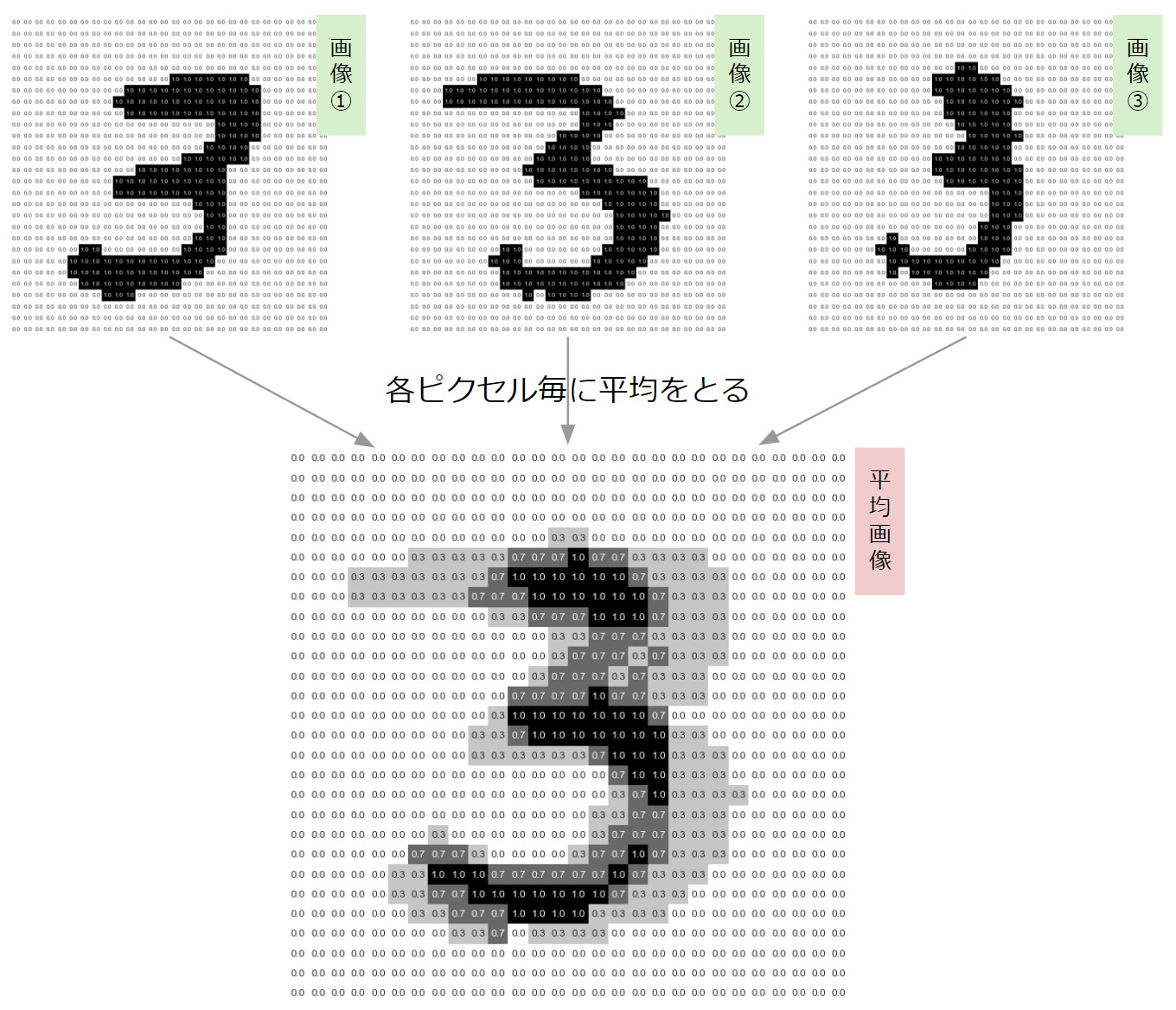
多くの画像で共通して手書きされたピクセルほど、ピクセル値が大きくなり、より黒く表示されています。逆に、あまり手書きされなかったピクセルは値が小さくなり、より薄いグレーとして表示されます。
上記の説明はもっともらしいものですが、さきほど説明した「画像生成器」とどのような関係があるのでしょうか?実は、この「代表画像」の各ピクセルの数値は、最尤推定で決定した「画像生成器」に一致します。この関係を次項で見ていきましょう。
代表画像と最尤推定法、画像生成器
例えば、先ほど得られた代表画像の各ピクセルの値を確率変数 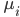
この確率 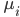
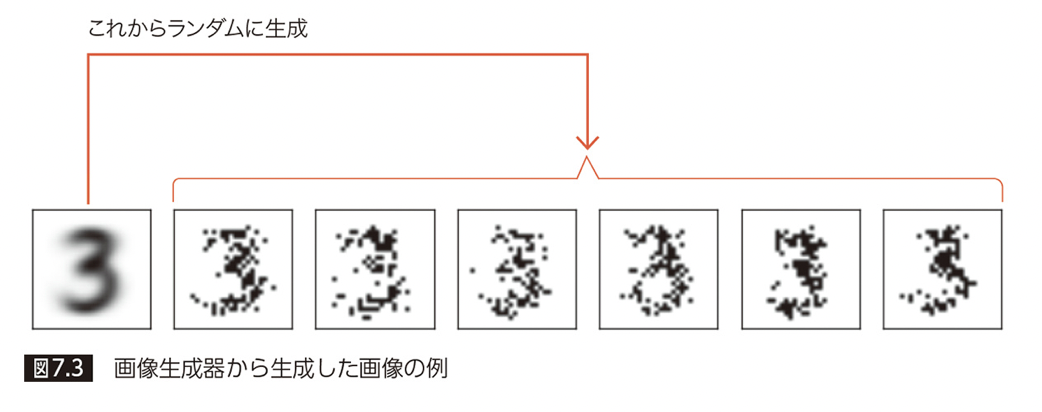
これが「画像生成器」の考え方ですが、ここで、画像生成器の精度を上げることを考えます。つまり、事前に与えられたデータにできるだけ類似した画像が生成できる画像生成器を考えます。すると、先ほどの「代表画像」がその答えになります。その理由は、次の通りです。
この画像生成器の精度を上げるということは、生成データと実際のデータが近いということです。普通に考えると、両者が一致する確率はかなり低いはずですが、この確率をできるだけ高めるように画像生成器をチューニングします。これには、3 章で説明した最尤推定法が利用できます。
最尤推定法は、「与えられたデータから計算される尤度関数を最大化する」という条件で、データの発生元となる確率分布のパラメータを求める方法でした。ここでは、尤度関数として、「生成データと実際のデータがすべて一致する確率」を採用します。これは、各ピクセルごとの確率 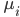
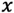
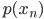
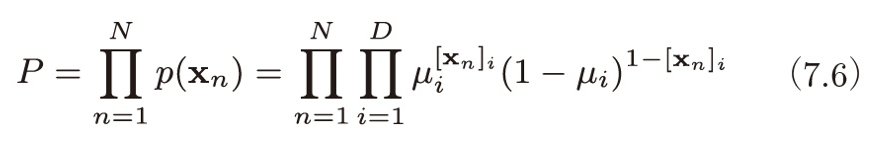
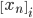
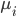
この式を最大化する 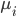
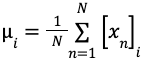
EM アルゴリズムで手書き文字の分類を行う
混合分布の場合の確率
代表画像や画像生成器、最尤推定法についてわかったところで、これらが EM アルゴリズムによる手書き文字分類にどう関わってくるのか説明します。
前節では、一つの数字に着目し、その画像生成器を作成しました。まず、これを拡張して、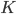
(数字が 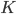
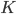
このとき、全部で 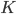
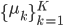
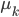
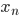
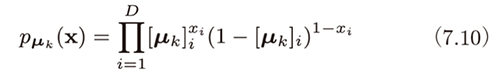
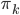
画像 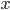
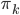
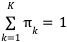
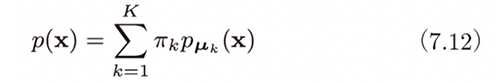
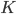
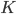
確率的に画像生成器を選択し、選択した画像生成器からランダムに生成される画像と実際のトレーニング画像が一致する確率(=尤度関数)は、具体的には、次式のようになります。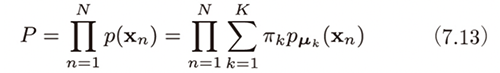
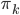
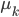
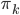
3 章の最尤推定法とは異なり、 
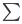

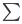
EM アルゴリズムによってパラメータを求める
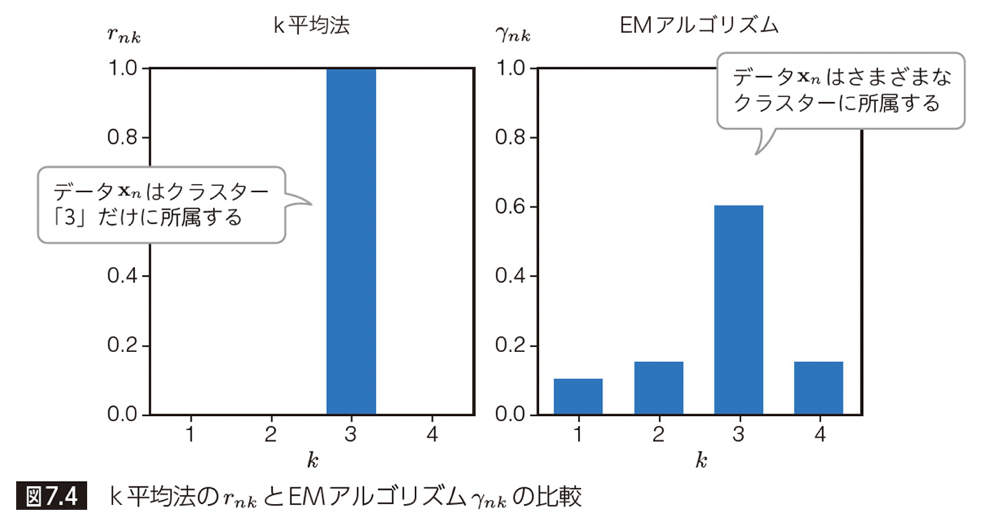
EM アルゴリズムは 6 章で説明した k 平均法 と類似した手続きによって尤度関数を最大化するパラメータを求めていきます。そのため、以下では k 平均法と対比する形で EM アルゴリズム の説明をしていきます。
k 平均法とは異なり、EM アルゴリズムはソフト・クラスタリングの手法であるため、一つではなく複数のクラスタに確率的に属します。例えば、以下に示す画像を分類するとします。多くの人がこの数字画像を「3」と答えるはずですが、人によっては「2」や「0」に分類するかもしれません。
(例:「3」に60%、「4」と「2」に15%ずつ、「1」に10%。)
具体的には、特定の k 番目の画像生成器から、画像 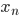
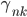
帰属確率 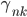
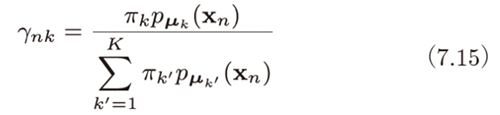
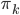
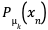
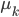
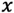
k 平均法では距離に着目して重心(=平均)を更新していましたが、EM アルゴリズムでは、この帰属確率 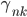
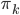
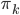
そして、(7.15) で計算される帰属確率 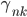
ここでは、それぞれの画像生成器が各クラスタの「代表点」になっているものと考えてください。
最後に、2 節の定義と本節の具体例とを対比します。文章だけだとなかなか難しい部分もありますが、こちらの表を見ると幾分整理されるのではと思います。
| 定義(2節) | 具体例(本節) | |
|---|---|---|
| ①Eステップ |
「隠れ変数」の期待値 を求める |
「πk(画像生成器を選択する確率)」 を求める |
|
確率モデルのパラメータ を固定し、 「隠れ変数の事後確率 (=モデルの尤度の期待値)」 を求める |
「μk(画像生成器)」 を固定し、 「πk(画像生成器を選択する確率)」の事後確率 を求める |
|
| ②M ステップ |
E ステップで求めた
「隠れ変数の事後確率 (=モデルの尤度の期待値)」 を踏まえて、 これを最大化するパラメータ を求める |
E ステップで求めた
「πk(画像生成器を選択する確率)」の事後確率 を踏まえて、 新たな「μk(画像生成器)」 を求める |
| ③反復 | M ステップで求めた
パラメータ を用いて 「隠れ変数」の分布 を再計算する |
M ステップで求めた
「μk(画像生成器)」 を用いて 「πk(画像生成器を選択する確率)」 を再計算する |
※ ①②③を収束するまで繰り返す。
まとめ
本章では、手書き数字の画像分類問題を通じて、EM アルゴリズムについて解説しました。
代表画像や画像生成器といった概念を通じて、観測不可能な潜在変数がある場合の最尤推定法である EM アルゴリズムの活用方法について理解が深まったのではないでしょうか。
EM アルゴリズムでクラスタ分類する際には、k 平均法と類似した部分と異なる部分があったかと思います。特に、k 平均法のようなハード・クラスタリングとは異なり、複数のクラスタに所属する確率が求まるソフト・クラスタリングという大きな違いがありました。
次章の第 8 章は、最尤推定からもう一歩進んだ、モデルのパラメータも確率的に考える「ベイズ推定」を紹介します。
参考リンク
※ Google Cloud は、Google LLC の商標です。
※ この記事は、本書籍で扱われているトピックについて、クラウドエースのメンバーが独自の見解で補足説明を加えたものになります。
| 章 | タイトル | 概要 |
|---|---|---|
| 1 | データサイエンスと機械学習 | ビジネスにおけるデータサイエンスの役割とデータサイエンスと機械学習の関係性を学ぶ |
| 2 | 最小二乗法: 機械学習理論の第一歩 | 「最小二乗法」で回帰分析を行い、機械学習の理論的な基礎となる「統計モデル」と基本のワークフローを理解する |
| 3 | 最尤推定法: 確率を用いた推定理論 | 「最尤推定法」で回帰分析を行い、確率を用いたモデルの役割について学ぶ |
| 4 | パーセプトロン: 分類アルゴリズムの基礎 | 分類アルゴリズムの基礎となる「パーセプトロン」と数値的計算手法の基礎となる確率的勾配降下法を学ぶ |
| 5 | ロジスティック回帰と ROC 曲線: 分類アルゴリズムの評価方法 | 最尤推定法を用いた分類アルゴリズムである「ロジスティック回帰」と分類アルゴリズムの評価方法について学ぶ |
| 6 | k 平均法: 教師なし学習モデルの基礎 | 「k 平均法」を用いて教師なし学習のクラスタリングについて学ぶ |
| 7 | EM アルゴリズム: 最尤推定法による教師なし学習 | 最尤推定法を用いた教師なしクラスタリングの手法として「EM アルゴリズム」を学ぶ |
| 8 | ベイズ推定: データを元に「確信」を高める手法 | 「ベイズ推定」で回帰分析を行う手法を学ぶ。ベイズ推定と最尤推定の違いを理解し、パラメータを確率的に推定するということを理解する |
クラウドエースとは
クラウドエースは Google Cloud 専門のシステムインテグレーターです。
Google Cloud の最先端の機械学習環境の活用について、豊富な知見を持つエンジニアがご要望にあわせて最適な形で技術支援をいたします。機械学習テクノロジーをご検討の際は、一度お気軽にお問い合わせください。
こちらの無料資料では、Google Cloud とクラウドエースについてさらに詳しく記載していますので、ぜひ合わせて御覧ください。

