
ITエンジニアのための機械学習理論入門
第 6 章 k 平均法:教師なし学習のモデルの基礎
こんにちは。クラウドエースのエンジニアの坂田です。
この記事は、Google Cloud 中井悦司さんの著書「IT エンジニアのための機械学習理論入門」の内容を参考に、機械学習の裏にある数学的な理論をわかりやすく紹介していきます。

昨今では、機械学習という技術がますます一般化されていますが、その分触れる事が少なくなった理論部分が、中井さんの書籍ではとてもわかりやすく解説されています。
ここでは特に重要と思われるポイントを、章ごとに記事としてまとめています。
「このような内容をもっと詳しく勉強したい!」と感じた方は、これらの記事を参考にしながら、中井さんの書籍を読んでいただければ、より深く掘り下げて理解を深めることができるでしょう。
本章の位置づけ
今までの章では教師あり学習のアルゴリズムについて触れてきましたが、第 6 章では教師なし学習のアルゴリズムの1つである「k 平均法(k-means)」について学びます。
k 平均法は、データの類似度に基づいてグループ分けをする「クラスタリング」と呼ばれるタスクに適用することができます。そして、k 平均法はクラスタ(後述)に「代表点」を設定し、代表点とデータの間の距離が小さい場合に「類似度が高い」と判定し、クラスタリングを行います。
この記事では、クラスタリングの基本的な考え方とk平均法の理論について説明します。また、 k 平均法を実装する際の注意点についてもご紹介します。
クラスタリングとは
「クラスタリング」は与えられたデータを似た者同士でグループ分けする手法で、教師なし学習の手法の1 つです。1 つ 1 つのグループは「クラスタ」と呼ばれます。教師あり学習の「分類」と少し似ていますが、教師あり学習は正解ラベルを元にデータを分類するのに対し、クラスタリングは正解ラベルなしでデータをグループ分けします。
図1 の犬と猫の画像の分類・クラスタリングの例を見ると、分類では「犬」「猫」といった正解ラベルが画像に付属していますが、クラスタリングでは画像に正解ラベルはありません。そのため、分類モデルは「ラベル」(またはその確率)を出力するのに対し、クラスタリングモデルは画像のグループ分けを行います。
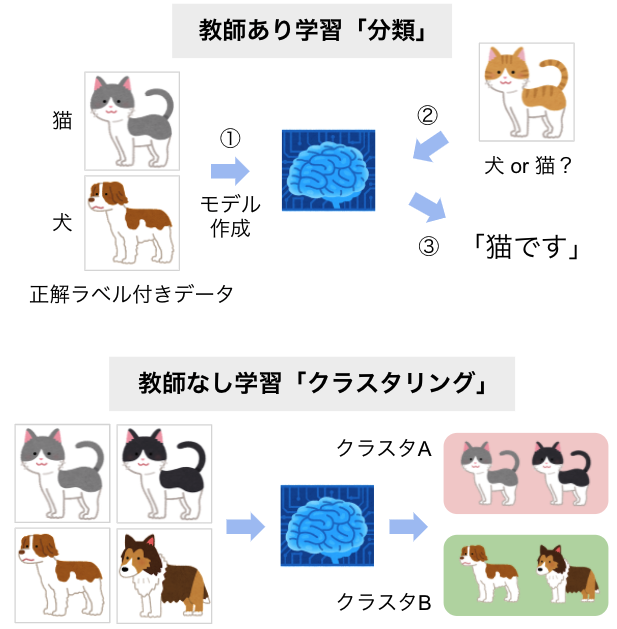
図 1 分類とクラスタリングの違い
クラスタリングではデータ同士の類似度を元にグループ分けを行います。今回紹介する「k 平均法」はクラスタの「代表点」を取り、代表点から各データまでの距離が短いほど類似度が高いと判断します。それでは k 平均法について具体的に見ていきましょう。
k 平均法
k 平均法とは、クラスタの「平均的な位置(重心)」を求めて、データを k 個のクラスタに分けるアルゴリズムです。どういうことなのか、k 平均法の具体的な手順を見ていきます。
k 平均法は以下に示す手順でクラスタリングを行います。
- 「何個のクラスタに分けるか」を設定する
- ランダムにクラスタの「代表点」を設定する
- データと代表点の「距離」を計算し、距離が最も近い代表点のクラスタにデータを所属させる
- クラスタの「重心」を新たな「代表点」とする
- (3)(4)を繰り返す
それでは、ステップごとに説明していきます。
(1) 「何個のクラスタに分けるか」を設定する
図 2 に示すように、今回のトレーニングセット(黒色の点)は xy 平面上に散らばっています。今回はこれらのデータを「2 個」のクラスタに分けたいと思います。なお、n 個のデータから構成されるトレーニングセットは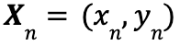
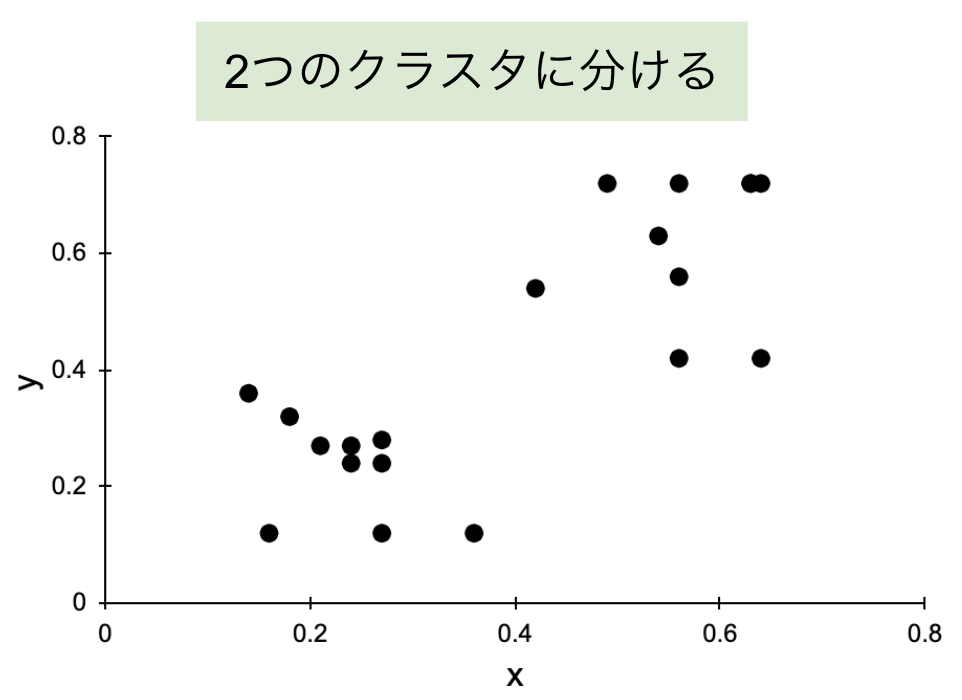
図 2 トレーニングセット
(2) ランダムにクラスタの「代表点」を設定する
次に、2 個のクラスタそれぞれの「代表点」をランダムに設定します。代表点は「クラスタの中心」を表し、データがどのクラスタに属するかを決める基準となるものです。ここでは、図 3 のように、青色の三角形と赤色の星形で示した点を代表点とし、2 つの代表点は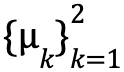
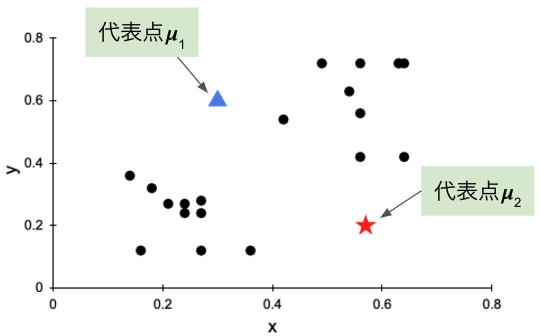
図 3 代表点
(3) データと代表点の「距離」を計算し、距離が最も近い代表点のクラスタにデータを所属させる
設定したクラスタの代表点とデータの間の「距離」をデータごとに求め、距離が最も近い代表点(クラスタ)にデータを所属させます(図 4)。距離は 2 点間の直線距離(ユークリッド距離といいます)で、次式で求めます。
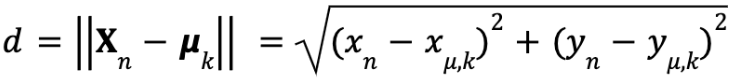
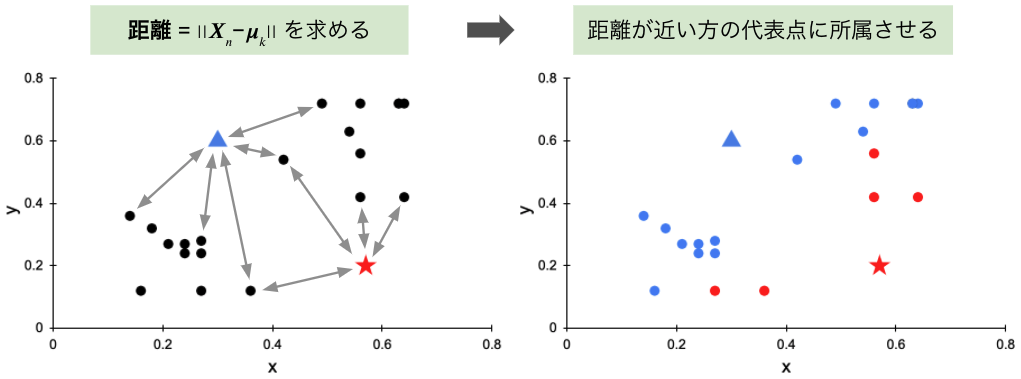
図 4 データと代表点の間の距離
(4) クラスタの「重心」を新たな代表点とする
図 4 の右を見ると、データは赤と青の 2 つのクラスタに分けられましたが、良い分け方とは言えません。より良い分け方をするために、クラスタの代表点の位置を更新します。新しい代表点はクラスタの「重心」とします。今回のデータは座標で表されるので、クラスタに所属するデータの座標をすべて足し合わせてクラスタのデータ数で割れば重心の座標を求めることができます。次式はk番目のクラスタの重心を求める式です。
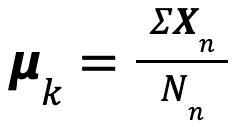
上記の式をもとに代表点を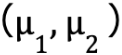
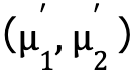
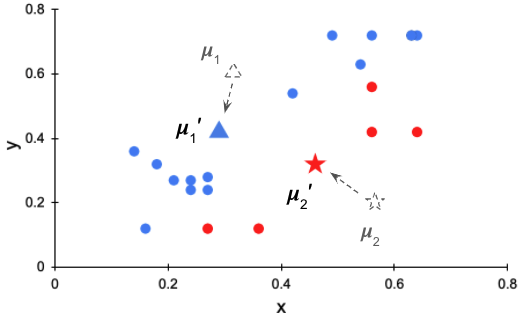
図 5 代表点を更新
(5) (3) (4) を繰り返す
代表点を更新したので、再び(3)を行ってクラスタを振り直します(図 6)。
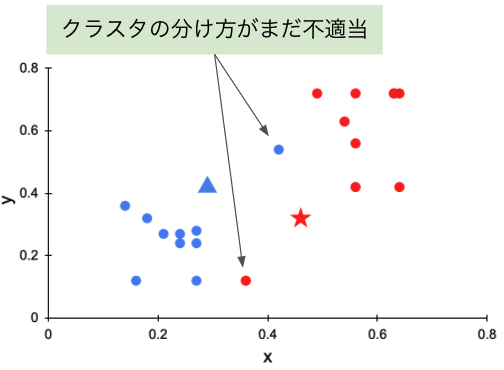
図 6 クラスタを振り直す
図 6 を見ると、クラスタの分け方はまだ不適当なようです。そのため、(4)を行って代表点を更新し、もう 1 度クラスタを振り分け、まだ駄目ならもう 1 度、というように(3)(4)を何度も繰り返していきます。そして、図 7 のように、無事にデータを適切に 2 つのクラスタに分けることができました。
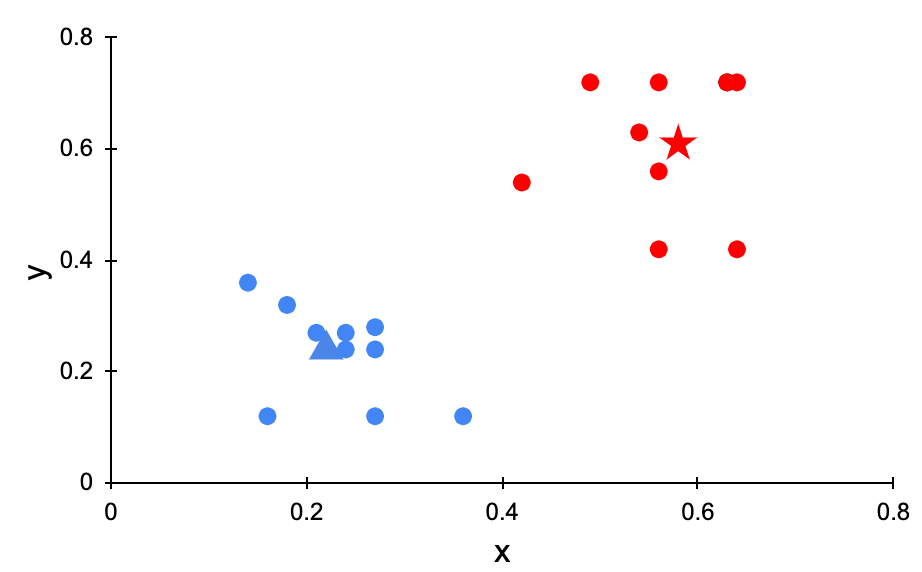
図 7 クラスタリングが成功
以上が k 平均法のアルゴリズムです。k 平均法はデータをクラスタに分ける際にはデータの重心が用いられます。重心は「データの平均的な位置」と言い換えることができ、データの平均的な位置を用いて任意の k 個のクラスタに分割するというところから、「k 平均法」という名前が付けられています。
一方で、k 平均法は比較的シンプルなアルゴリズムであるため、使用する際に注意するべきポイントもあります。
k 平均法の注意点
今回の例は(x,y)の 2 次元のデータなので可視化がしやすく、クラスタの分け方を確認しながらクラスタリングを行うことができましたが、いつも可視化できるとは限りません。
では、(3)(4)の繰り返しの回数は何を基準にして決定すればいいのでしょうか。実は、代表点は最終的にどこかしらの位置に定まります。そのため、基本的にクラスタリングの状況を可視化しながらクラスタリングを行う必要は無く、代表点の更新をある程度の回数を行えばクラスタリングが完了します。
しかし、k 平均法を実装する際には次の 2 つの点に注意する必要があります。
(1) 常に最適なクラスタに分けられるわけではない
代表点の更新を何回も行えば最終的に特定の場所に定まると述べましたが、その特定の場所が最適な位置とは限りません。実は最終的に収束する場所は、最初にランダムに決定した代表点の位置によって変化し、モデルの性能も上下します。そのため、k 平均法では、代表点の初期値を変化させながら何回もクラスタリングを行い、最も良い性能を示したモデルを採用することが必要となります。
また、書籍には書いていませんが、モデルの性能が初期値に依存する問題を克服するために考案された「k-means++」という手法も存在します。気になる方は是非調べてみてください。
(2) 代表点が定まるまで時間がかかる場合がある
代表点の更新を何回も行えば最終的に特定の場所に定まりますが、時間がかかってしまう場合があります。機械学習において、学習の時間を短縮するというのは 1 つの課題でもあります。解決策として、以下の 2 つが挙げられます。
- 代表点の更新の回数を 20 回や 50 回などと決め打ちする
- 代表点がある程度動かなくなったら途中で打ち切る
本書では、2 つ目を採用していて、「ある程度動かなくなる」の基準に「2 乗歪み」を採用しています。2 乗歪みは代表点と各データの距離の 2 乗の総和であり、次式で表されます。
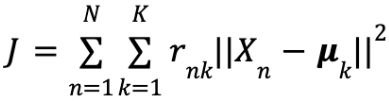
このJが極小値をとるとき、代表点は 1 点に定まります。上式の数学的な裏付けは書籍にお任せしますが、書籍ではこの J の値の変化が小さくなったら代表点の更新を打ち切るという形になっています。以上のように、k 平均法では何かしらの基準を設けて途中で打ち切ることが多いです。
5. まとめ
この記事では、教師なし学習のクラスタリングについて簡単におさらいし、第 6 章で登場した k 平均法についてご紹介しました。また、k 平均法の注意点についてもご紹介しました。
また、書籍の第 6 章では、k 平均法 (k-means) の他に「k 近傍法 (k-NN, k-nearest neighbor algorithm)」という手法も登場します。
名前が似ていますが、
k 平均法は教師なし学習のクラスタリング手法であるのに対し、
k 近傍法は教師あり学習の分類手法という点で全く違います。
k 近傍法について気になる方は是非書籍を手に取ってみてください。
次の第 7 章ではクラスタリングに最尤推定法を取り入れた「EM アルゴリズム」が登場します。
※ Google Cloud は、Google LLC の商標です。
※ この記事は、本書籍で扱われているトピックについて、クラウドエースのメンバーが独自の見解で補足説明を加えたものになります。
- 第 5 章:ロジスティック回帰とROC 曲線
- (公開予定)第 7 章: EM アルゴリズム
| 章 | タイトル | 概要 |
|---|---|---|
| 1 | データサイエンスと機械学習 | ビジネスにおけるデータサイエンスの役割とデータサイエンスと機械学習の関係性を学ぶ |
| 2 | 最小二乗法: 機械学習理論の第一歩 | 「最小二乗法」で回帰分析を行い、機械学習の理論的な基礎となる「統計モデル」と基本のワークフローを理解する |
| 3 | 最尤推定法: 確率を用いた推定理論 | 「最尤推定法」で回帰分析を行い、確率を用いたモデルの役割について学ぶ |
| 4 | パーセプトロン: 分類アルゴリズムの基礎 | 分類アルゴリズムの基礎となる「パーセプトロン」と数値的計算手法の基礎となる確率的勾配降下法を学ぶ |
| 5 | ロジスティック回帰と ROC 曲線: 分類アルゴリズムの評価方法 | 最尤推定法を用いた分類アルゴリズムである「ロジスティック回帰」と分類アルゴリズムの評価方法について学ぶ |
| 6 | k 平均法: 教師なし学習モデルの基礎 | 「k 平均法」を用いて教師なし学習のクラスタリングについて学ぶ |
| 7 | EM アルゴリズム: 最尤推定法による教師なし学習 | 最尤推定法を用いた教師なしクラスタリングの手法として「EM アルゴリズム」を学ぶ |
| 8 | ベイズ推定: データを元に「確信」を高める手法 | 「ベイズ推定」で回帰分析を行う手法を学ぶ。ベイズ推定と最尤推定の違いを理解し、パラメータを確率的に推定するということを理解する |
クラウドエースとは
クラウドエースは Google Cloud 専門のシステムインテグレーターです。
Google Cloud の最先端の機械学習環境の活用について、豊富な知見を持つエンジニアがご要望にあわせて最適な形で技術支援をいたします。機械学習テクノロジーをご検討の際は、一度お気軽にお問い合わせください。
こちらの無料資料では、Google Cloud とクラウドエースについてさらに詳しく記載していますので、ぜひ合わせて御覧ください。


