
ITエンジニアのための機械学習理論入門
第2章 最小二乗法: 機械学習理論の第一歩
こんにちは。クラウドエース技術本部 Data / ML Division の坂田です。
この記事は、Google Cloud 中井悦司さんの著書「IT エンジニアのための機械学習理論入門」の内容を参考に、機械学習の裏にある数学的な理論をわかりやすく紹介していきます。

昨今では、機械学習という技術がますます一般化されていますが、その分触れる事が少なくなった理論部分が、中井さんの書籍ではとてもわかりやすく解説されています。
ここでは特に重要と思われるポイントを、章ごとに記事としてまとめています。
「このような内容をもっと詳しく勉強したい!」と感じた方は、これらの記事を参考にしながら、中井さんの書籍を読んでいただければ、より深く掘り下げて理解を深めることができるでしょう。
本章の位置づけ
回帰分析は統計学および機械学習の代表的な手法の一つで、最小二乗法は回帰分析を実現するために用いられる基礎的な手法の一つです。
回帰アルゴリズムの機械学習モデルを理解する上で、最小二乗法は避けて通れないでしょう。
この記事では、機械学習について「学習の手法」「モデル作成の流れ」「学習時に考慮すべき問題」の 3 つの観点から第 2 章を説明し、学習の手法として「最小二乗法」、モデル作成の流れとして「パラメトリックモデル」、学習時に考慮すべき問題として「オーバーフィッティング」について取り上げます。
| 学習の手法 | 最小二乗法 |
|---|---|
| モデル作成の流れ | パラメトリックモデル |
| 学習時に考慮すべき問題 | オーバーフィッティング |
上記 3 つのポイントを押さえると機械学習の基本的なワークフローが見えてきます。
それでは順番に追っていきましょう。
はじめに:機械学習とは
最小二乗法の説明の前に、まずは簡単に機械学習についておさらいします。
ご存知の方は読み飛ばしてください。
機械学習の手法は大きく分けて、「教師あり学習」と「教師なし学習」の 2 つがあります。教師あり学習は、機械学習モデルに「正解のデータ」(正解ラベル、教師データと呼ばれます)を与えて学習させる手法です。
機械学習は「あるデータを用いて、ある事柄を説明するモデル」を作成することが目的であり、教師あり学習では「あるデータ」は「特徴量」、「ある事柄」は「正解ラベル」に呼びます。(また統計学では特徴量を「説明変数」、正解ラベルを「目的変数」と呼びます。)
学習には、学習の大元となる「トレーニングセット」と呼ばれるデータが必要となります。トレーニングセットには、特徴量と正解ラベルのペアが複数含まれます。
学習は以下の流れで行います(図 1)。
- モデルに特徴量を入力する
- モデルから出力を得る
- モデルの出力と正解ラベルを比較し、出力が正解ラベルに近づくようにモデルを調整する
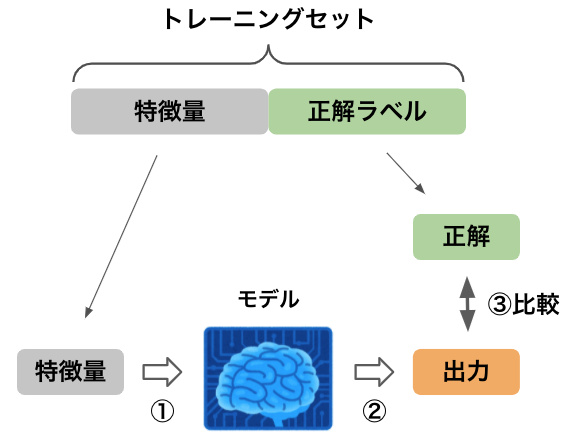
図 1 トレーニングセットと学習の流れ
上記の中で、3 ステップ目の「出力が正解ラベルに近づくようにモデルを調整する」という部分で、最小二乗法が登場します。
学習の手法:最小二乗法
それでは、最小二乗法について見ていきましょう。
結論から言うと、最小二乗法とは「モデルの予測値(出力)と正解ラベル(正解)の二乗誤差が最小となるように関数のパラメータを決定する手法」です。
つまり「モデルの出力と正解の『差』ができるだけ小さくなるようにモデルを調整する手法」です。
どういうことなのか、第 2 章の例題を用いて説明します。
初めに 10 組のデータ (x , t) を考えます。x は特徴量で、t は正解ラベルです(図 2の青点)。
例題のゴールは 図2 の緑色の実線のグラフで示すような、「t を x で説明するモデル=関数」を求めることです。
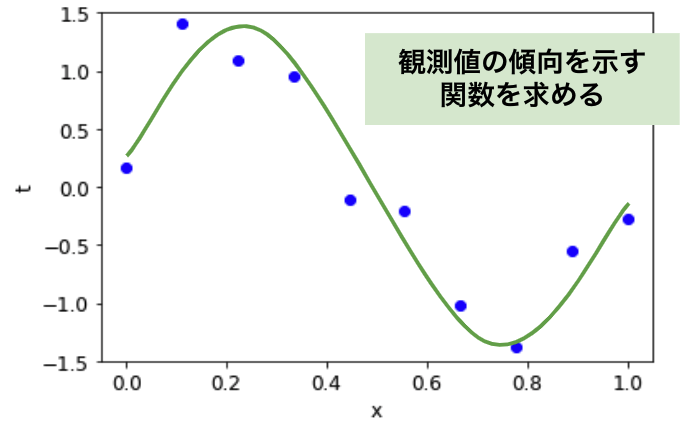
図 2 観測値と求める関数のグラフ
では、モデル=関数はどうやって求めるのでしょうか。
まずは t を x で説明する関数としてf ( x ) を仮定します。本書では次式のようなパラメータとして w と M を持つ M次多項式を定義しています。
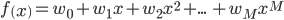
この関数のパラメータである、w と M を求めることで関数(モデル)は完成します。(パラメータwは最小二乗法で求め、パラメータMは人間の手で求めます。)
最小二乗法のイメージとしては、M の値を決定した上で、w の値を変化させて 図 3 の緑色の実線のグラフの形を変化させ、赤色の点線で示した青点とグラフの「距離」が最小になるグラフの形(= パラメータ)を求めるのです。
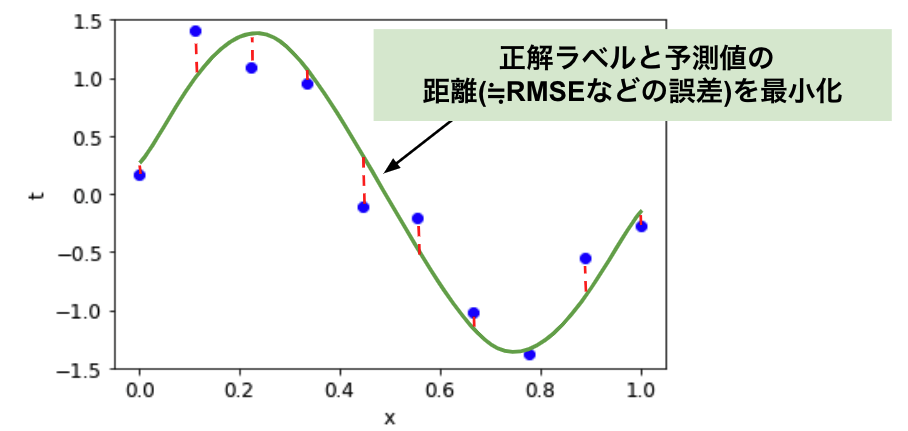
図 3 誤差
実際には、赤色の点線のような「距離」ではなく、次式で表されるような「平方根平均二乗誤差( RMSE : Root Mean Squared Error )」などの「二乗誤差」と呼ばれる値を最小化するようにパラメータを求めます。
この二乗誤差を最小化することから、この手法は「最小二乗法」と呼ばれています。
また、RMSE など、最小化の対象となる誤差を求める関数は「損失関数」と呼ばれています。
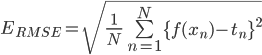
第 2 章の例では、パラメータwは解析的に求めることができます。
損失関数を最小化するパラメータwは、以下の式で表されるように、損失関数(例えば、ERMSE)をwの関数とみなした際の偏微分係数が 0 となるという条件で決定されます。この記事では説明を省きますが、以下の式を解いていくことでwが求まります。
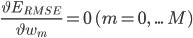
一方で、パラメータMは先ほど述べたように、計算などで求められるものではなく、人間が決定する必要があるものです。
パラメータの内、人間が決定するものを「ハイパーパラメータ」と呼びます。
ハイパーパラメータは様々な候補を用意しておき、その中からモデルが最も良い性能を示したハイパーパラメータを採用します。
以上をまとめると、最小二乗法は「目的変数を説明変数で説明する関数を仮定し、損失関数の値が最小となるようなパラメータを求め、関数を決定する手法」ということができます。
モデル作成の流れ:パラメトリックモデル
統計学的な手法を用いて何らかの現象(データ)を説明・予測するためのものを「統計モデル」と言います。
その中でも特に、最小二乗法で求める関数のように、パラメータをもつモデルをパラメトリックモデルと言います(厳密にはパラメータを持った確率分布を用いたモデルのことを指します)。
パラメトリックモデルは以下の流れで決定します。
- パラメータを含むモデル(数式)を設定する
- パラメータを評価する基準を定める
- 最良の評価を与えるパラメータを決定する
パラメトリックモデルのようなパラメータを持つ統計モデルを最適化する(目的変数を説明変数で正しく説明できるようにする)ということは、パラメータを最適化するということです。
そして、機械学習モデルも同様にパラメータを持つため、機械学習モデルの最適化は、パラメータの最適化と同義です。
ゆえに、パラメトリックモデルと機械学習モデルは類似していることから、パラメトリックの流れを理解することで機械学習モデルの流れを理解することに繋がります。
「回帰アルゴリズムの多項式モデルを最小二乗法で最適化する」という第 2 章の例では、以下の流れでモデルを決定します。
- M次多項式を仮定するパラメータ w を解析的に求める
- パラメータの評価基準として RMSE を使用する
- RMSE の値を元にパラメータMを決定する
学習時に考慮すべき問題:オーバーフィッティング
オーバーフィッティング(過学習)とは、モデルがトレーニングセット(学習用に与えられたデータ)に過剰に適合(フィッティング)してしまい、未知のデータ(テストセット)に対してはモデルの性能が低下してしまう状態を指します。
オーバーフィッティングは機械学習では考慮すべき代表的な問題であり、以下の 2 つの観点から対処します。
5-1. オーバーフィッティングを検出する
5-2. オーバーフィッティングを防ぐ
オーバーフィッティングを検出する
オーバーフィッティングの検出にはトレーニングセットとは別に用意した「テストセット」を使用します。
通常は、用意したデータをトレーニングセットとテストセットに分割します。
モデルはトレーニングセットだけで学習し、トレーニングセットとテストセットそれぞれに対する損失関数の値を計算・比較します( 図 4 )。
トレーニングセットとテストセットそれぞれに対する損失関数の値に大きな差が出た場合、オーバーフィッティングが疑われます(通常はテストセットの方が悪い値になります)。
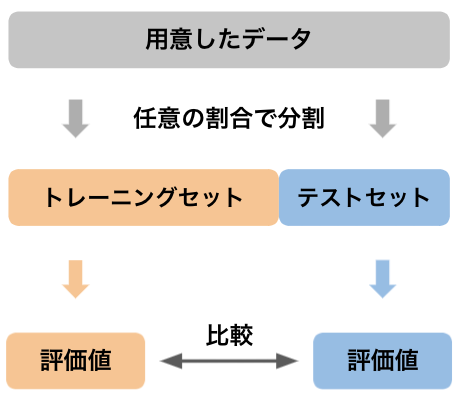
図 4 モデルの検証
図5 はトレーニングセットとテストセットに対する RMSE(予測誤差)の推移を示しています。
M の値が 3 より大きくなると、テストセットの RMSE(予測誤差)の方が大きくなり、その差がどんどん開いていくことが分かります。
このことから、M が 3 より大きいときはオーバーフィッティングの可能性があると言えます。
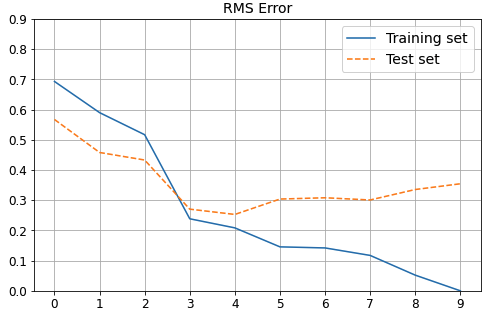
図 5 予測誤差の推移
また、用意したデータをトレーニングセットとテストセットに分割する際、複数のパターンで分割を行い、モデルの検証を複数回行う検証手法もあります。
これは「クロスバリデーション(交差検証)」と呼ばれ、データの分割の際に発生しやすい「データの偏り」を防ぐことができ、より効果的にオーバーフィッティングを検出することができます。
クロスバリデーションでは複数の検証結果が得られるため、それらの結果を平均するなど、結果を総合的に見てモデルの状態を判断します(図 6)。
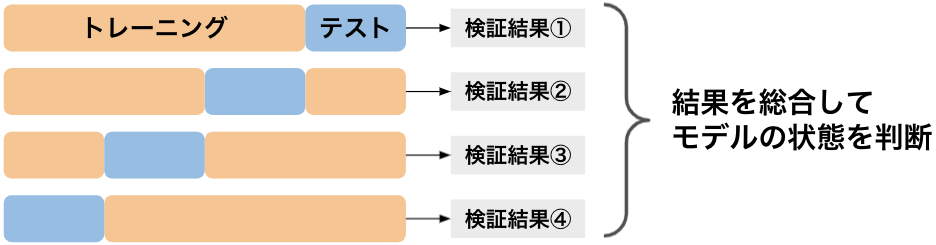
図 6 クロスバリデーション
テストセットに用いた検証の結果、最良なパラメータが決定できた場合は、トレーニングセットとテストセットを結合し、用意したすべてのデータを使用してモデルを作成、モデルの本番稼働へと向かいます。
オーバーフィッティングを防ぐ
オーバーフィッティングを防ぐ手法はたくさん存在しますが、ここではシンプルな手法として以下の 2 つをご紹介します。
A)ハイパーパラメータを調整する
B)データ数を増やす
A)ハイパーパラメータを調整する
第 2 章の例では、パラメータMがハイパーパラメータでした。
図 7 に M=0,1,3,9 ときのモデルのグラフ(赤色の実線)を示します。
E の値が最も良いのは M=9 のときですが、グラフはトレーニングセット(青色の点)をすべて通る形になっており、データの本質的な特徴を掴めているとは言えません。
これは明らかにオーバーフィッティングです。
一方、M=3 のときは、E の値は M=9 のときよりも悪い値になっているものの、グラフはデータの特徴をうまく捉えています。
このように、ハイパーパラメータの調整でモデルの性能が向上し、オーバーフィッティングを防ぐことができます。
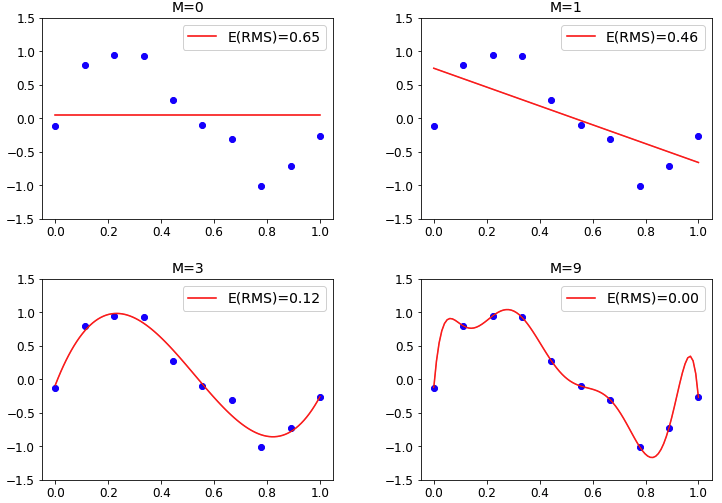
図 7 パラメータMの調整
今回の例ではグラフを描くことができたので、オーバーフィッティングを目で確かめることができました。
しかし、いつもグラフを描けるとは限らないので、上でも述べたように、オーバーフィッティングかどうかはトレーニングセットとテストセットの予測誤差を比較して確かめます。
B)データ数を増やす
トレーニングセットのデータ数とオーバーフィッティングには関係があります。
データが少なすぎるとデータが偶然持っていた特徴を掴みやすくなってしまい、オーバーフィッティングになりやすくなります。
そのため、データ数を増やすとデータの本質的な特徴を捉えることができるようになり、オーバーフィッティングが起きにくくなります(図 8)。
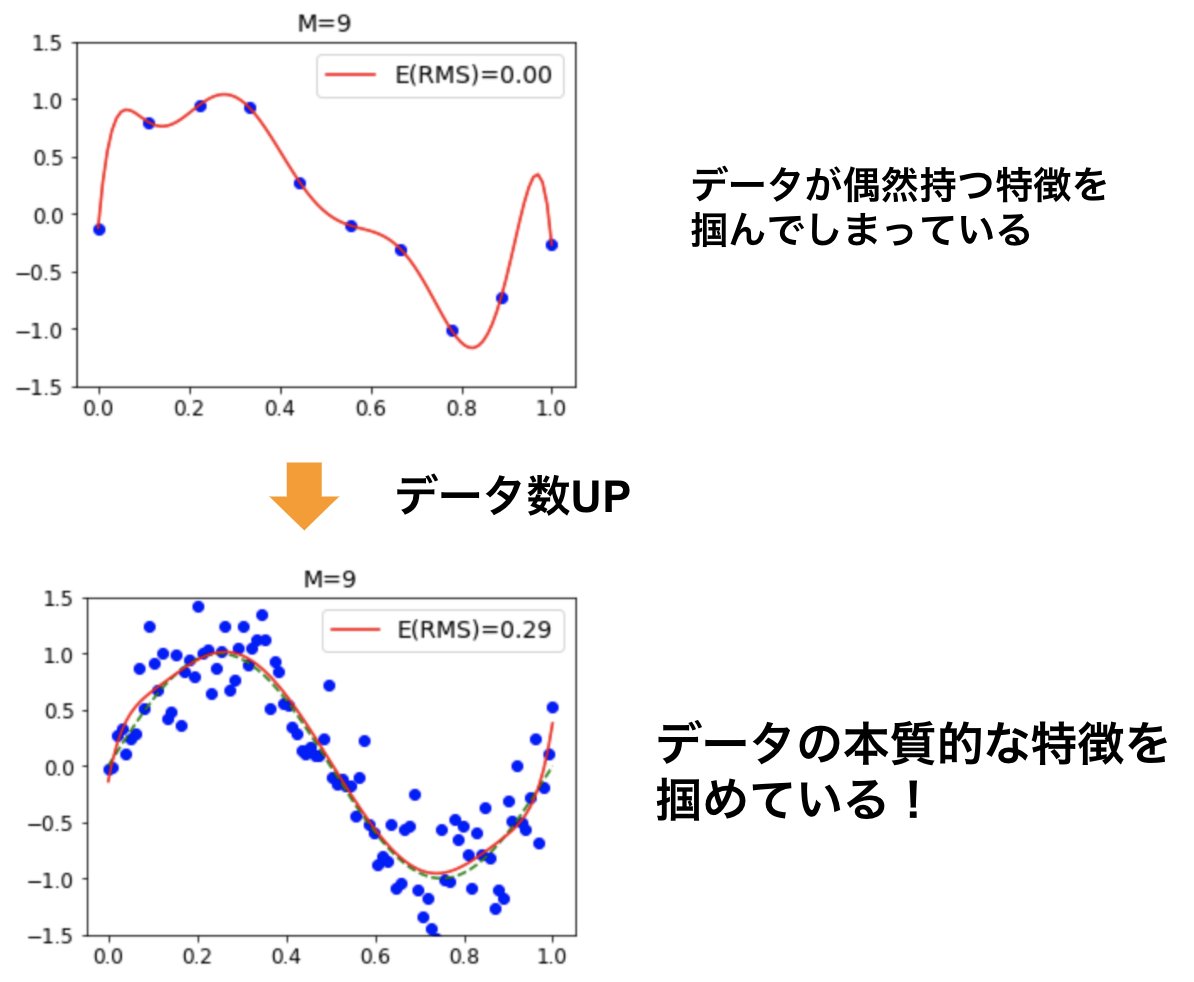
図 8 データ数を増やす
まとめ
第 2 章ではまず、回帰分析の基本である最小二乗法について学びました。
次に、モデル作成のガイドラインとなるパラメトリックモデルについて学びました。最後に、機械学習で考慮すべき代表的な問題であるオーバーフィッティングについて学びました。
第 2 章の 3 つのポイントをまとめると、機械学習の基本的なワークフローが見えてきます。
- データを用意し、トレーニングセットとテストセットに分割する
- 機械学習に使用するモデルを決定する
- パラメータを評価する基準を定める
- テストセットを用いて検証を行う
- 最良の評価を与えるパラメータを決定する
機械学習は基本的に上記の流れで行います。
その上で、機械学習モデルの性能をあげるため、それぞれのステップにおいて様々な手法が考案されています。
今後の章でその様々な手法を学んでいきましょう。
次の第 3 章では確率を用いてパラメータの推定を行う手法である「最尤推定法」が登場します。
| 章 | タイトル | 概要 |
|---|---|---|
| 1 | データサイエンスと機械学習 | ビジネスにおけるデータサイエンスの役割とデータサイエンスと機械学習の関係性を学ぶ |
| 2 | 最小二乗法: 機械学習理論の第一歩 | 「最小二乗法」で回帰分析を行い、機械学習の理論的な基礎となる「統計モデル」と基本のワークフローを理解する |
| 3 | 最尤推定法: 確率を用いた推定理論 | 「最尤推定法」で回帰分析を行い、確率を用いたモデルの役割について学ぶ |
| 4 | パーセプトロン: 分類アルゴリズムの基礎 | 分類アルゴリズムの基礎となる「パーセプトロン」と数値的計算手法の基礎となる確率的勾配降下法を学ぶ |
| 5 | ロジスティック回帰と ROC 曲線: 分類アルゴリズムの評価方法 | 最尤推定法を用いた分類アルゴリズムである「ロジスティック回帰」と分類アルゴリズムの評価方法について学ぶ |
| 6 | k 平均法: 教師なし学習モデルの基礎 | 「k 平均法」を用いて教師なし学習のクラスタリングについて学ぶ |
| 7 | EM アルゴリズム: 最尤推定法による教師なし学習 | 最尤推定法を用いた教師なしクラスタリングの手法として「EM アルゴリズム」を学ぶ |
| 8 | ベイズ推定: データを元に「確信」を高める手法 | 「ベイズ推定」で回帰分析を行う手法を学ぶ。ベイズ推定と最尤推定の違いを理解し、パラメータを確率的に推定するということを理解する |
クラウドエースとは
クラウドエースは Google Cloud 専門のシステムインテグレーターです。
Google Cloud の最先端の機械学習環境の活用について、豊富な知見を持つエンジニアがご要望にあわせて最適な形で技術支援をいたします。機械学習テクノロジーをご検討の際は、一度お気軽にお問い合わせください。
こちらの資料では、Google Cloud とクラウドエースについてさらに詳しく記載していますので、ぜひ合わせて御覧ください。


