
ITエンジニアのための機械学習理論入門
第 5 章 ロジスティック回帰と ROC 曲線: 分類アルゴリズムの評価方法
こんにちは。クラウドエースのエンジニアの坂田です。
この記事は、Google Cloud 中井悦司さんの著書「IT エンジニアのための機械学習理論入門」の内容を参考に、機械学習の裏にある数学的な理論をわかりやすく紹介していきます。

昨今では、機械学習という技術がますます一般化されていますが、その分触れる事が少なくなった理論部分が、中井さんの書籍ではとてもわかりやすく解説されています。
ここでは特に重要と思われるポイントを、章ごとに記事としてまとめています。
「このような内容をもっと詳しく勉強したい!」と感じた方は、これらの記事を参考にしながら、中井さんの書籍を読んでいただければ、より深く掘り下げて理解を深めることができるでしょう。
この章の位置づけ
第 5 章では、第 3 章で登場した最尤推定法を分類アルゴリズムに応用した「ロジスティック回帰」と分類アルゴリズムの評価方法について学んでいきます。
図1 犬と猫の分類
ロジスティック回帰は最尤推定法を応用した分類アルゴリズムであるため、「ある事象が発生する確率」を得ることができます。例えば、犬と猫の画像の分類を行うタスクについて考えると、ロジスティック回帰モデルは犬(または猫)である「確率」を出力します。
パーセプトロンとの違いとして、第 4 章で登場したパーセプトロンのモデルはデータのラベルを出力するのに対し、ロジスティック回帰はデータがそのラベルである確率を出力するという点があげられます。
また、第 5 章ではロジスティック回帰だけでなく、分類アルゴリズムの評価方法についても学びます。 分類アルゴリズムでは「しきい値」の設定が必要になります。しきい値とは、先ほどの犬と猫の分類の例においては、猫である確率が何%以上であるときに「猫である」と判断するのかという判定条件にあたります。また、複数の分類モデルを作成した場合、モデル同士の性能を比較する必要があります。第 5 章では、こういった、「しきい値の設定」や「モデルの性能評価」を行うために使用する「ROC 曲線」や「PR 曲線」について触れていきます。
この記事では、ロジスティック回帰の仕組みに関する理論的な内容と、分類アルゴリズムの評価方法に関する実践的な内容についてご紹介します。
ロジスティック回帰
ロジスティック回帰は最尤推定法を用いてモデルのパラメータを決定します。ここでは第 3 章の最尤推定法についておさらいしつつ、第 5 章の例題を用いてロジスティック回帰のモデル作成の流れを説明していきたいと思います(第 3 章の最尤推定法の解説記事はこちら)。
ロジスティック回帰のモデルはパラメトリックモデルなので、これまでに何度も登場した以下のパラメトリックモデルの 3 ステップでモデルを決定します。
- パラメータを含むモデル(数式)を設定する
- パラメータを評価する基準を定める
- 最良の結果を与えるパラメータを決定する
そして、ロジスティック回帰は最尤推定法を用いた手法なので、最尤推定法と同じ流れでモデルを決定します。パラメトリックモデルの 3 ステップにならうと、最尤推定法は以下の方法でモデルを決定します。
- 求めたいモデル(関数)を定義する
- 尤度関数を定義する
- 尤度関数の値が最大となるようにモデルのパラメータを求める
上記の流れでロジスティック回帰のモデルを作成していきます。
(1) 求めたいモデル(関数)を定義する
今回の例は、図 2 のように (x, y) 平面上に散らばった 2 種類のデータ(青色の丸とオレンジ色のバツ)を分類するというものです。求める関数はこの2種類のデータ(トレーニングセット)を分類する直線を表す1次関数で、次式で表します。
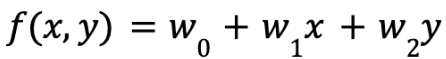
f(x,y)=0 のとき、データの分割線が決定します。つまり、f(x,y)=0 のときのパラメータ w を求めることがゴールです。このパラメータ w は最尤推定法を用いて求めます。そのためにまずは尤度関数を定義します。
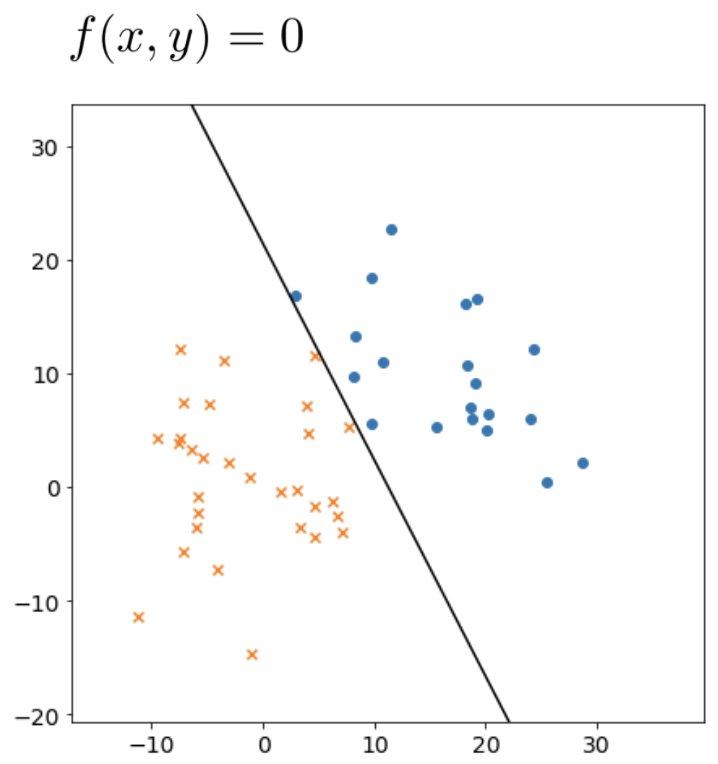
図2 2 種類のデータを分割する直線 f(x,y)=0
(2) 尤度関数を定義する
「尤度」とは、ある前提条件によってある事象(データ)が発生する場合、発生した事象から考えて前提条件を評価する指標です。もう少し具体的に説明すると、尤度は仮定した前提条件 θ の下でデータ X が発生する確率を示す「条件付き確率」です。
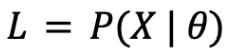
この尤度が大きいとき、データ X から考えて前提条件 θ は「尤もらしい(理にかなっている)」と考えることができます。今回の例では、データ X は「トレーニングセット」、前提条件 θ は「モデル」です。つまり、あるモデル(のパラメータ)を仮定したときに、「トレーニングセットがモデルから得られる確率」が尤度で、尤度の値を見ることでパラメータの良し悪しを判断することができます。
そして、「尤度関数」は前提条件 θ(モデルのパラメータ)がパラメータである関数のことを指します。最尤推定法は、この尤度関数の値が最大値を取るときのモデルのパラメータを最終的なパラメータとして採用する手法です。
それでは、尤度関数である「トレーニングセットがモデルから得られる確率の式」を定義していきます。
まず、青色の点について考えます。データの分割線が図3 の直線の位置にあると仮定したとき、「点が青色の点である確率」は分割線を直交する赤色の矢印の方向(右上)に行くにつれて大きくなり、矢印と反対方向(左下)に行くにつれて小さくなります。分割線上(f(x,y)=0)が青色の点である確率は 50% です。
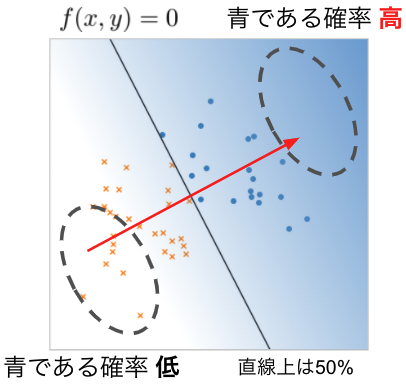
図3 青色の点である確率
「青色の点である確率」は赤色の矢印の方向に 0 から 1 になめらかに変化します。そして、f(x,y) の値は -∞ から ∞ に線形で変化するため、青色の点である確率と f(x,y) を対応させて、確率の分布を示すグラフを図4のように表すことができます。
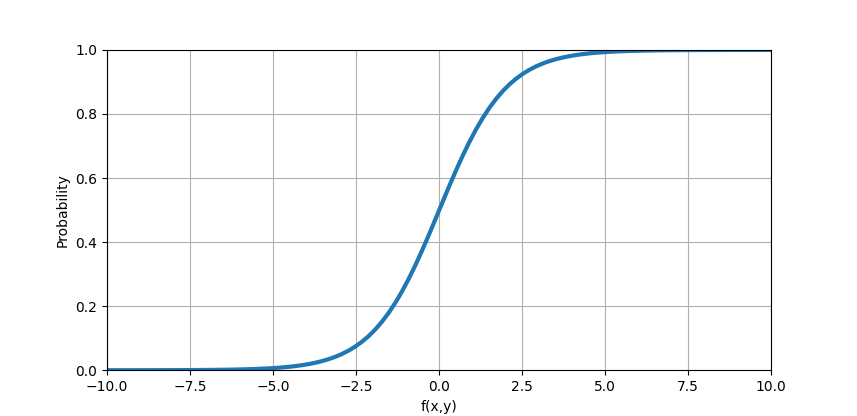
図4 青色の点である確率の分布
0 から 1 になめらかに変化するグラフは「ロジスティック関数」と呼ばれる次式で表すことができます。
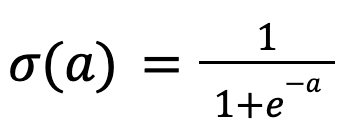
ロジスティック関数はロジット関数の逆関数です。ロジット関数とは、オッズ(ある事象が起きる確率と起こらない確率の比)に対数を取った対数ロジットの関数です。
余談ですが、ロジスティック関数は図4 のように S 字(ギリシャ文字でシグマ)の形のグラフを描くことから、シグモイド関数とも呼ばれ、記号にシグマが用いられます。
このロジスティック関数を用いると、青色の点である確率 P(x,y) は次式になります。
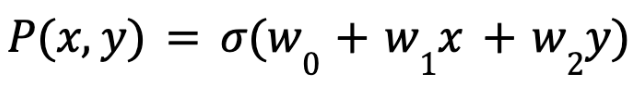
さらに、青色の点を t=1、オレンジ色の点を t=0 とすると、特定の点のデータ 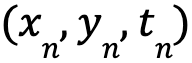
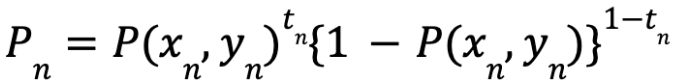
特定の点ではなく、トレーニングセット全体で考えると、「トレーニングセットがモデルから得られる確率」は上式の積として次式で表せます。
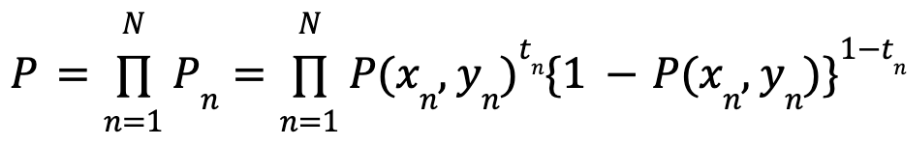
この w をパラメータとする P の式が尤度関数です。
最後に、尤度関数 P が最大値を取るときのパラメータ w を求めていきます。
(3) 尤度関数の値が最大となるようにモデルのパラメータを求める
今回定義した尤度関数 P は複雑な数式であるため、w を解析的に求めることはできません。今回は、第 4 章のパーセプトロンで用いた「勾配降下法」ではなく「ニュートン・ラフソン法」と呼ばれる手法でパラメータを近似的に求めますが、詳細な説明は書籍にお任せすることとします。
分類アルゴリズムの予測結果と評価方法
前節では直線上のデータが青色である確率が 50%、オレンジ色である確率も 50% となるようにモデルを作成しました。すなわち、データの分類の基準を以下のように定めたということです。
- 青色である確率が 50% 以上のとき: データの属性は青色
- 青色である確率が 50% 未満のとき: そのデータの属性はオレンジ色
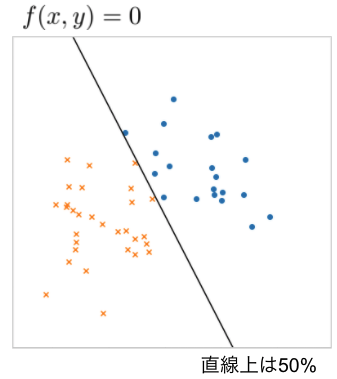
図5 データを分割する直線
では、分類の「しきい値」である 50% という値は果たして妥当なものなのでしょうか。分類アルゴリズムでは、分類の基準となるしきい値を、しっかりとした根拠をもとに人間の手で決める必要があります。
また、複数の分類モデルを作成した場合、モデルの性能を評価し、モデル同士を比較する必要も出てきます。
このような「しきい値の設定」や「分類モデルの性能評価」の際、「ROC 曲線」や「PR 曲線」といった指標のグラフ化が役に立ちます。ここからは、まず分類モデルの予測結果の見方について説明した後、ROC 曲線や PR 曲線について説明します。
分類モデルの予測結果としきい値
分類モデルのしきい値を変化させるとモデルの性能も変化します。しきい値を変えるということは、図 6 のように、データを分割する直線の位置を変更することに相当します。

図6 しきい値の変更
図 6 を見ると、分割線の位置によっては、本来の属性(色)とは逆の属性と判断されてしまうデータが存在することがわかります。とは言いつつ、2 種類のデータを完璧に分ける直線を引くことは難しいようです。そのため、「モデルによる誤った判断」をある程度許容する必要があります。どの程度許容するかの判断は、分類タスクなどによって異なり、難しい判断になる場合もあります。その判断の材料として、予測結果を一覧化した「混同行列」というものがあります。
混同行列とは以下の表のように表されるものです。
表1 分類結果の組み合わせ(混同行列)
| Predicted: 陽性 | Predicted: 陰性 | |
|---|---|---|
| Actual: 陽性 | 真陽性 | 偽陰性 |
| Actual: 陰性 | 偽陽性 | 真陰性 |
分類問題において、発見したいデータの属性を「陽性」、そうでない属性を「陰性」と呼びます。例えば、「感染症の検査」で考えると、感染している状態が陽性、感染していない状態が陰性と言えます。一方で、検査によって陽性か陰性を完璧に分類できない場合、検査結果は陽性だとしても、実際は感染していないという場合が考えられます(その逆も)。そのため、分類結果(検査結果)と実際の属性(実際の感染の有無)の組み合わせは上記の表の 4 通りが存在します。そして、分類結果が上記の表のどれに当てはまるかをカウントし、カウント数を表に当てはめたものが「混同行列」になります。
モデルによる分類結果を上記の 4 通りに振り分けて、誤った分類をした「偽陽性」や「偽陰性」の割合が多い場合、そのモデルの性能は低い(そのしきい値は良くない値である)ということになります。
この混同行列から指標を計算し、指標をもとに作成するのが次に説明する「ROC 曲線」や「PR 曲線」です。これらを用いることでしきい値の設定の判断が行いやすくなります。また、ROC 曲線や PR 曲線はモデルの性能を定量的に評価できるため、分類モデル同士の比較も可能になります。
ROC 曲線
実際は陽性であるデータの内、正しく陽性と判断されたデータの割合を「真陽性率(再現率、Recall)」、逆に実際は陰性であるデータの内、誤って陽性と判断されたデータの割合を「偽陽性率」と呼びます。真陽性率と偽陽性率は以下の式で計算します。

例えば、感染症の検査で考えると、真陽性率は「実際に感染している人を正しく陽性と判断できる割合」、偽陽性率は「非感染者を誤って陽性と判断する確率」と言えます。
ROC 曲線(Receiver Operatorating Characteristic curve)とは、縦軸に真陽性率、横軸に偽陽性率を取って、様々なパターンのしきい値のときの真陽性率と偽陽性率をプロットしたときに描かれる曲線のことです(図 5)。
基本的に、ROC 曲線は図5のように左下から右上にかけてカーブを描くような形になります。
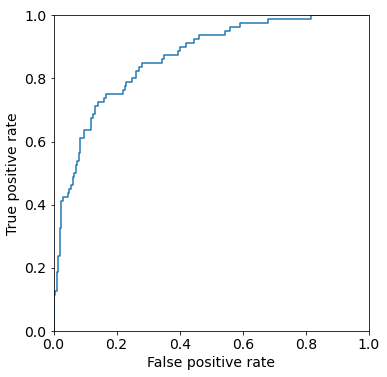
図5 ROC 曲線の例
ROC 曲線を見ると、真陽性率と偽陽性率はトレードオフの関係にあることが分かります。例えば、真陽性率を上げるためにしきい値を変化させる(ROC 曲線の右上の点を採用する)と偽陽性率も高くなります。その逆もしかりで、偽陽性率を下げようとすると真陽性率も下がってしまいます。
そのため、ROC 曲線を見ながら、真陽性率と偽陽性率が良い”あんばい”となるしきい値を探ることになります。
また、分類アルゴリズムにおいて、陽性であるデータをすべて陽性と判断し、陰性であるデータをすべて陰性と判断する状態が最も理想的な状態と言えます。つまり、真陽性率は 1、偽陽性率は 0 となり、ROC 曲線においては左上の場所です。このことから、ROC 曲線がより大きく左上に張り出しているモデルは性能が良いと言えます。
そのため、ROC 曲線の形からモデルの性能を評価することができます。一般的には、ROC 曲線そのものの形ではなく、ROC 曲線と横軸との間の面積の大きさ「AUC(Area Under the Curve)」を使用して性能評価を行い、モデル同士の比較を行います(図 6)。
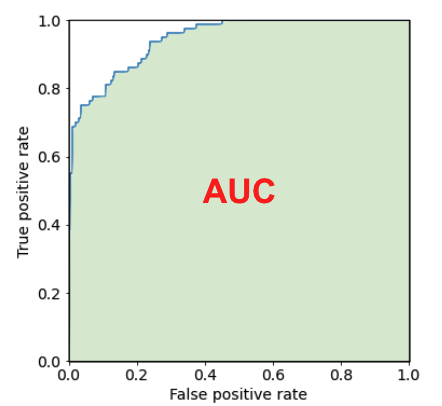
図6 AUC
PR 曲線
ROC 曲線と似たものとして、PR 曲線(Precision-Recall Curve)があります。
PR 曲線は縦軸に「適合率(Precision)」、横軸に「真陽性率(再現率:Recall)」を取り、様々なパターンのしきい値の場合の点をプロットしたときに描かれる曲線です(図 7)
適合率は以下の式で求めます(真陽性率も再掲します)。

感染症の検査の例だと、適合率は「陽性と判断された人の中で、実際に感染している人の割合」、真陽性率は「実際に感染している人を正しく陽性と判断できる割合」と言えます。
つまり、真陽性率は「陽性と判断すべきデータをどれだけ陽性と判断できたか(網羅性)」を示し、適合率は「陽性と判断したデータの内、どれだけ正しい判断ができたか(正確性)」を示しています。
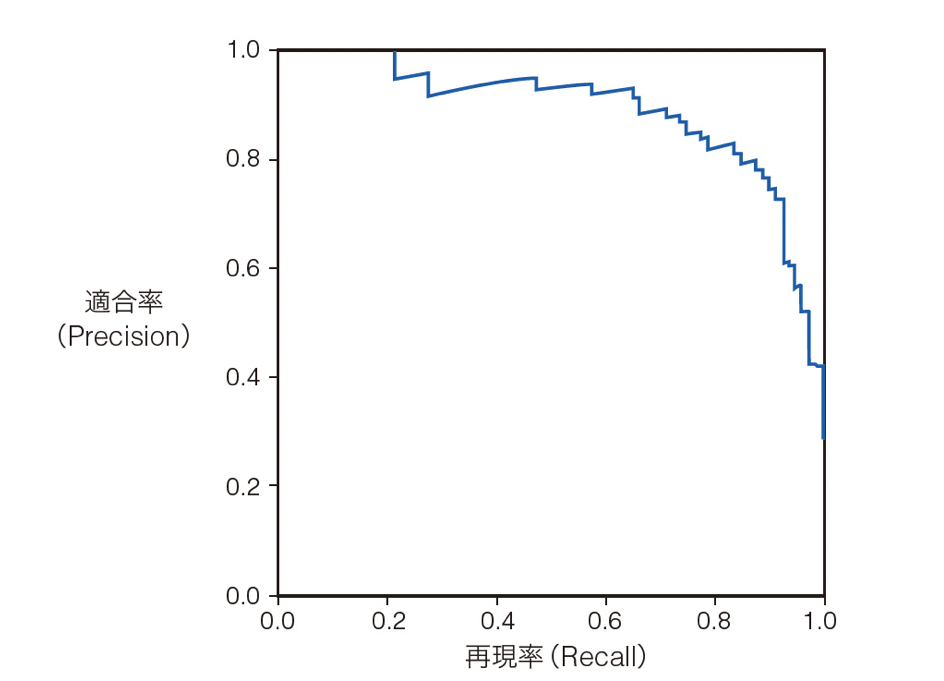
図7 PR 曲線
PR 曲線は右上に張り出しているほど、性能が高いことを示しています。完全に右上に張り出している(曲線が正方形になる)場合は、実際に陽性であるデータをすべて陽性と判断し、陽性と判断したデータはすべて実際に陽性であるという理想的な状態です。ROC 曲線と同様に面積の大きさ(AUC)で定量的にモデルの性能を判定することができます。
ROC 曲線と PR 曲線の違い
ROC 曲線は陽性と陰性の両方を見ているのに対し、PR 曲線は陽性だけを見ているという点に違いがあります。基本的には、しきい値の設定やモデルの評価に、 ROC 曲線と PR 曲線のどちらも使用します。しかし、ROC 曲線には注意すべき点もあります。
ここで、一例として、「非常に珍しい病気を発見するための検査」について考えます。この場合、トレーニングデータの陽性データ(病気にかかっている)が陰性と比べ極端に少なくなります。陽性データが少ない場合、「正しく陰性と分類する」パターンが多くなり、陽性データを正しく分類できなくても、ROC 曲線だと性能が良いように見えてしまいます。
そのため、このような「陰性に比べて陽性が極端に少ない」場合は、陽性だけを見る PR 曲線を活用した方がよいでしょう。
まとめ
第 5 章では、まず前半で分類アルゴリズムであるロジスティック回帰について学びました。ロジスティック回帰は、モデルのパラメータを最尤推定法で決定し、分類結果は確率で表現されます。
後半では、分類アルゴリズムの予測結果の特徴とモデルの評価手法に関して、ROC 曲線や PR 曲線を用いたしきい値の設定やモデルの性能評価について学びました。
今回は理論的な内容だけでなく、分類アルゴリズムの評価という実践的な内容もありました。第 5 章の内容は分類モデルを作成するときにきっと役に立つはずです。
次の第 6 章では教師なし学習の「k 平均法」が登場します。
※ Google Cloud は、Google LLC の商標です。
※ この記事は、本書籍で扱われているトピックについて、クラウドエースのメンバーが独自の見解で補足説明を加えたものになります。
| 章 | タイトル | 概要 |
|---|---|---|
| 1 | データサイエンスと機械学習 | ビジネスにおけるデータサイエンスの役割とデータサイエンスと機械学習の関係性を学ぶ |
| 2 | 最小二乗法: 機械学習理論の第一歩 | 「最小二乗法」で回帰分析を行い、機械学習の理論的な基礎となる「統計モデル」と基本のワークフローを理解する |
| 3 | 最尤推定法: 確率を用いた推定理論 | 「最尤推定法」で回帰分析を行い、確率を用いたモデルの役割について学ぶ |
| 4 | パーセプトロン: 分類アルゴリズムの基礎 | 分類アルゴリズムの基礎となる「パーセプトロン」と数値的計算手法の基礎となる確率的勾配降下法を学ぶ |
| 5 | ロジスティック回帰と ROC 曲線: 分類アルゴリズムの評価方法 | 最尤推定法を用いた分類アルゴリズムである「ロジスティック回帰」と分類アルゴリズムの評価方法について学ぶ |
| 6 | k 平均法: 教師なし学習モデルの基礎 | 「k 平均法」を用いて教師なし学習のクラスタリングについて学ぶ |
| 7 | EM アルゴリズム: 最尤推定法による教師なし学習 | 最尤推定法を用いた教師なしクラスタリングの手法として「EM アルゴリズム」を学ぶ |
| 8 | ベイズ推定: データを元に「確信」を高める手法 | 「ベイズ推定」で回帰分析を行う手法を学ぶ。ベイズ推定と最尤推定の違いを理解し、パラメータを確率的に推定するということを理解する |
クラウドエースとは
クラウドエースは Google Cloud 専門のシステムインテグレーターです。
Google Cloud の最先端の機械学習環境の活用について、豊富な知見を持つエンジニアがご要望にあわせて最適な形で技術支援をいたします。機械学習テクノロジーをご検討の際は、一度お気軽にお問い合わせください。
こちらの無料資料では、Google Cloud とクラウドエースについてさらに詳しく記載していますので、ぜひ合わせて御覧ください。

