ITエンジニアのための機械学習理論入門

こんにちは。技術本部 DataML Division の高鳥です。
この記事は、Google Cloud 中井悦司さんの著書「IT エンジニアのための機械学習理論入門」の内容を参考に、機械学習の裏にある数学的な理論をわかりやすく紹介していきます。

昨今では、機械学習という技術がますます一般化されていますが、その分触れる事が少なくなった理論部分が、中井さんの書籍ではとてもわかりやすく解説されています。ここでは特に重要と思われるポイントを、章ごとに記事としてまとめています。「このような内容をもっと詳しく勉強したい！」と感じた方は、これらの記事を参考にしながら、中井さんの書籍を読んでいただければ、より深く掘り下げて理解を深めることができるでしょう。

本章の位置づけ

第8章では、「ベイズ推定」と呼ばれる考え方に基づき、機械学習モデル（回帰分析）を解いていきます。
ベイズ推定とは「とある条件における事象の確率を、既知の確率と観測データから求める手法」です。（この章の副題である「データを元に『確信』を高める手法」もこの意でしょう。）
この考え方は、今までの確率的な考え方（最尤推定等）と大きく異なります。
したがって、まずベイズ推定とは何か、ベイズ推定の考え方の基軸であるベイズ定理から詳しく説明していきます。ベイズ推定の概念を説明したあと、モデルのパラメータを評価するのにベイズ推定がどの様に活用できるのかを解説していきます。

ベイズの定理

ベイズ推定は、ベイズの定理と呼ばれる考え方を基本として推定を行います。よって、ベイズ推定を理解するためには、まずベイズの定理を理解する必要があります。
本節では、最初にベイズの定理と呼ばれる式を説明し、次にベイズの定理を具体例を交えて解説し、最終的にベイズの定理の意味を深く考えていきます。

まずはベイズの定理を見ていきましょう。

ベイズの定理は、確率変数を X , Y として「ある条件 X を前提とした場合の Y の確率を、確率P(Y | X) = 条件付き確率」と表現すると以下の様になります。

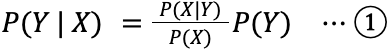
この式は、X と Y が同時に起きる確率 P (X,Y)の関係を、2 つの方法で表現することで簡単に導くことができます。

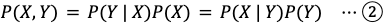
上式が成り立つ理由も簡単に説明しておきましょう。
P(Y|X)P(X) とは、X が起きた上での Y が起きる確率 P(Y|X)と考えられるので P(X,Y) と一致します。Y,X を取り替えても当然成り立つので、②の式が成り立つわけです。

サイコロを例にしてみましょう。実際にでる値を X 、偶数 or 奇数を Y とします。
P(X=1, Y=奇数) = 1/6  ですが、「奇数が出る確率P(Y=奇数) = 1/2」と「数が奇数の値(1,3,5) の中で値が 1 である確率 P(X=1 | Y=奇数) = 1/3」をかけ合わせて求めることもできます。

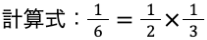
①の導出に戻ります。②から①を導出するには、全体を P(X) で割るだけです。

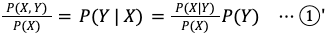
さて、この定理は何の役に立つのでしょうか？

実は、この定理を活用することで「とある条件における事象の確率を、既知の確率と観測データから求める」ことができます。

例えば、「ある病気の検査キットで陽性が出たとき、実際に陽性である確率がどれぐらいなのか」ということを考えてみましょう。
この確率を直接測定することは難しいでしょう。なぜなら、検査で陽性である人を最初から見つけるのは不可能に近いからです。しかし、ベイズの定理を用いることで、感染している／していない人へ検査の結果から検査キットの性能を求めることが可能になります。

具体的な数値で実際にやってみましょう。以下のような状況を想定します。

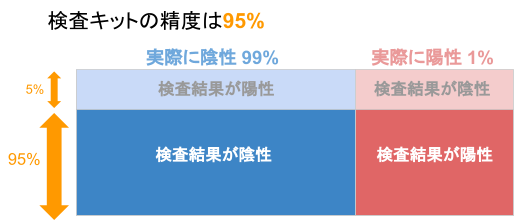
• 病気に感染している確率は 1 %
• 検査キットの精度は 95 %
  感染している人が正しく陽性と出る確率が 95 %
  感染していない人が正しく陰性と出る確率が 95 %

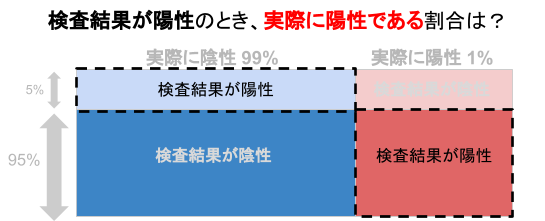
計算のために、状況を記号で表現します。
「実際に感染しているかどうか」を Y、「検査の結果」を X として立式します。

• 病気に感染している確率
  P( Y = 感染 ) = 0.01 ⇔ P( Y = 非感染 ) = 0.99
• 感染している人が正しく陽性と出る確率
  P( X = 陽性 | Y = 感染) = 0.95 ⇔ P( X = 陰性 | Y = 感染) = 0.05
• 感染していない人が正しく陰性と出る確率
  P(X = 陰性 | Y = 非感染) = 0.95 ⇔ P(X = 陽性 | Y = 非感染) = 0.05

求めたい確率「検査キットで陽性が出たとき、実際に陽性である確率」は P( Y = 感染 | X = 陽性)ですが、ベイズの定理①をつかうと次の様に表現されます。

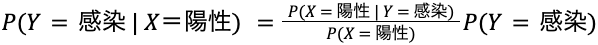
式を見ればわかるのですが、「P(X = 陽性)」以外は既に求まっています。また、唯一求まっていない「P(X = 陽性)」も、以下のように Y ごとで総和 Σ を取ることで間接的に求めることができます。

よって、最終的には、以下のような計算で結果が求まります。

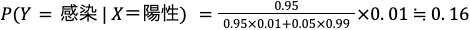
陽性反応があっても 16% 程度しか実際には感染していないということがわかりました。（逆に言うと、この検査をすれば通常 1 % の確率を 16 % まで引き上げるとも言えます。）

この様に、ベイズの定理は「前提条件がない場合に事象 Y が起こる確率 P(Y) = 事前確率」がわかっているとして、「ある条件 X を前提とした場合の確率 P(Y | X) = 条件付き確率」を求める際に使用します。これは、最初に述べた「とある条件における事象の確率を、既知の確率と観測データから求める」に当てはめると「とある条件 X における事象 Y の確率 P(Y|X)を、既知の確率 P(Y)と観測データから求める」とも言えます。
この「観測データから」の部分は「事象 Y が起きるときに条件 X であった確率 = P(X|Y)」と書き表します。というのも、推定したい事象 Y をとある条件 X でサンプリングした際に求まる確率だからです。

概して、元々わかっていた確率 P(Y)から、ある観測データの結果 P(X|Y)を元に、推定している事象 Y が起きる確率の確信度を高めていく手法といえます。

ベイズ推定

ベイズの定理を用いて、確率分布のパラメータを推定するのがベイズ推定になります。ベイズ推定と最尤推定との最大の違いは、推定するパラメータが確率分布として推定され一意に定まらないということです。

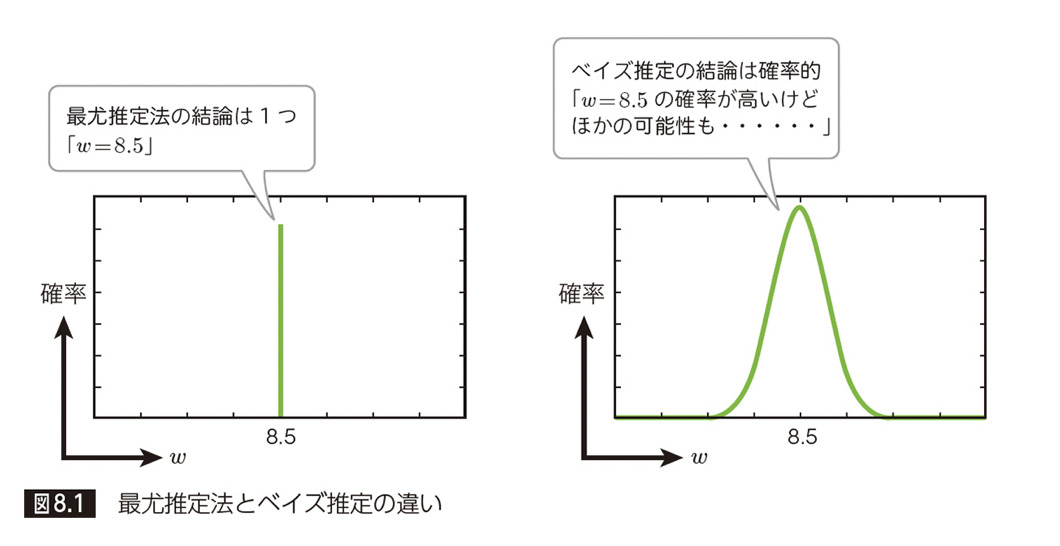
【図8.1】

「第3章 最尤推定法」の復習ですが、最尤推定法は、観測データの発生確率が最も高くなる確率分布のパラメータを推定します。具体的には、以下の様な尤度関数 P と呼ばれる式を最大化するパラメータを求めました。
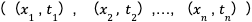
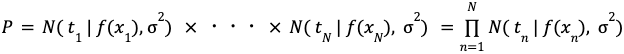
（観測データ をとし、分散σのガウス分布から発生するとしています。）
それに対し、ベイズ推定は、パラメータの値 u を確率分布として表現した上で、既知の分布 P(u) に対し観測データ t を元に分布を更新します。この更新された分布 P(u | t) の中で、最も確率が高い値、つまり、P(u | t) が最大となる u を推定値とします。

この更新は、求めたいパラメータを u ,データを t とおくと、ベイズの定理より、事前分布 P(u)に尤度関数 P(t | u)を掛ける計算になります。（なお、P(t)の部分は定数になるため、計算時には考慮する必要はありません。）
結果求まった事後分布 P(u | t)から、この分布を最大化する u を推定することができるわけです。

ベイズ推定の回帰分析への応用

さて、ベイズ推定を用いて、回帰分析を解いていきましょう。回帰分析の式を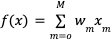 とすれば、求めたいパラメータは w になります。
この wを、与えられた観測データ tを元にどんどん更新していくわけです。式としては、③式の u を w に変えた以下の式になります。
更新する上で最大化したい確率は勿論 P(w | t)になりますが、具体的に最適化したい式がまだわかりません。実際に解いて明らかにしていきましょう。

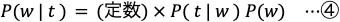
w の事前分布 P(w)及び t の発生分布 P(t | w)は、全て正規分布 N を仮定します。
（以降の式では t , w  が全てベクトルだと考えてください。）
t の発生分布は、最尤推定のときに最適化した式（尤度関数）と一致するので、具体的には、以下のような式になります。（ を利用して、総乗の を総和の に変換出来ることを利用しています。）
ここで は最小二乗法で用いた誤差関数と一致することに注意です。
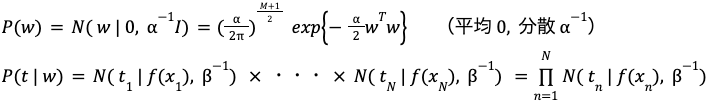
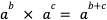
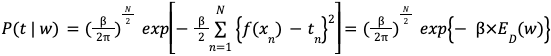
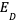
④式にこれらを代入して整理する（exponentialの次数と定数項をまとめる）と、次の式になり、最適化するべき関数が明らかになります。
見ての通り、この式の exponential に現れている次数が最適化する誤差関数 E(w)になります。
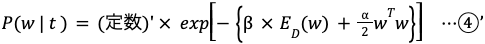
（④’式より、E(w)を最小化すれば P(w | t)は最大化します。）
この式を解くと求めたい w を導出することが可能です。
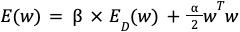
この式で注目したいことは、α を 0 にする、つまり事前分布の分散を大きくすると最尤推定の式に近づくということです。

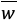
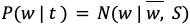
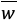
事後分布 P(w | t)の結果にも注意が必要です。事後分布の形も事前分布と同じく正規分布になります。この正規分布の平均を 分散を S とおくと以下の式になります。
この と S の具体的な式は本書におまかせしますが、観測データによって分布のパラメータが更新されたと考えることが可能です。

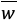
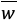
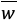
また、 はパラメータ w の平均を表したベクトルです。事後分布 P(w | T)を最大化する w は分布の平均 ですので、求めたいパラメータ w は となります。

まとめ

さて本書の最終章でしたが、いかがでしたか？
回帰アルゴリズムとして今まで紹介した話を理解した上で、さらにベイズ推定を新たに組み合わせたので、少々難しかったかもしれません。また、ベイズ推定がベイズの定理①を前提にするため、説明の大半が数式でとっつきにくく感じたかもしれません。
しかし、この式がやりたいことは極めてシンプルです。事前分布に対し観測データで更新をかけ、事後分布を求めるということです。具体的な手順は、事前分布に観測データが得られる確率を掛けると事後分布に比例 ∝ するということを利用しました。（定数項は計算する際に利用していないため、本質的にはこの比例関係だけで推定を行っています。）

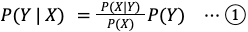
（事後分布） ∝（観測データが得られる確率） ×（事前分布）

そして、最も大事なことは、予めわかっていることや仮説を事前分布として推定に利用する事ができるということです。この”事前知識”のパラメータ α が誤差関数にも現れています。

誤差関数におけるこのパラメータ α は、一般にオーバーフィッティングを避けるための罰則項と考えられていますが、事前分布から定まるということがわかれば、より正確に定める事ができます。（詳細は本書に記載されています。）

このように理論を紐解くことで、モデルのハイパーパラメータの選択すらもより正確に行うことが出来るようになる場合があります。
本書は、機械学習の基礎理論を全てカバーしているわけではありませんが、基礎中の”基礎”理論が多く紹介されています。機械学習の理論を知る第一歩として、本書は適切な書物ではないかと思います。これから機械学習を学ぼうと思っている方や、本格的な専門書では挫折してしまった方も今一度、本書とともに第一歩を踏み出してみるのも良いかもしれません。

※ Google Cloud は、Google LLC の商標です。
※ この記事は、本書籍で扱われているトピックについて、クラウドエースのメンバーが独自の見解で補足説明を加えたものになります。

• • 第 7 章： EMアルゴリズム

クラウドエースとは

クラウドエースは Google Cloud 専門のシステムインテグレーターです。

Google Cloud の最先端の機械学習環境の活用について、豊富な知見を持つエンジニアがご要望にあわせて最適な形で技術支援をいたします。機械学習テクノロジーをご検討の際は、一度お気軽にお問い合わせください。

こちらの資料では、Google Cloud とクラウドエースについてさらに詳しく記載していますので、ぜひ合わせて御覧ください。

• シェアする
• ツイートする
• シェアする
• ブックマークする

• #AI・機械学習
• #tech系

合わせて読みたい