
ITエンジニアのための機械学習理論入門
第 4 章 パーセプトロン: 分類アルゴリズムの基礎
こんにちは。技術本部 DataML Division の高鳥です。
この記事は、Google Cloud 中井悦司さんの著書「IT エンジニアのための機械学習理論入門」の内容を参考に、機械学習の裏にある数学的な理論をわかりやすく紹介していきます。

昨今では、機械学習という技術がますます一般化されていますが、その分触れる事が少なくなった理論部分が、中井さんの書籍ではとてもわかりやすく解説されています。ここでは特に重要と思われるポイントを、章ごとに記事としてまとめています。「このような内容をもっと詳しく勉強したい!」と感じた方は、これらの記事を参考にしながら、中井さんの書籍を読んでいただければ、より深く掘り下げて理解を深めることができるでしょう。
本章の位置づけ
第 4 章では、これまでの章と異なり、「回帰」ではなく「分類」アルゴリズムについて見ていきます。具体的なアルゴリズムとしては、「パーセプトロン」と呼ばれる線形分類器の一種について取り上げます。線形分類器とは、簡単に言うと「直線によって分割した結果で分類する」アルゴリズムです。
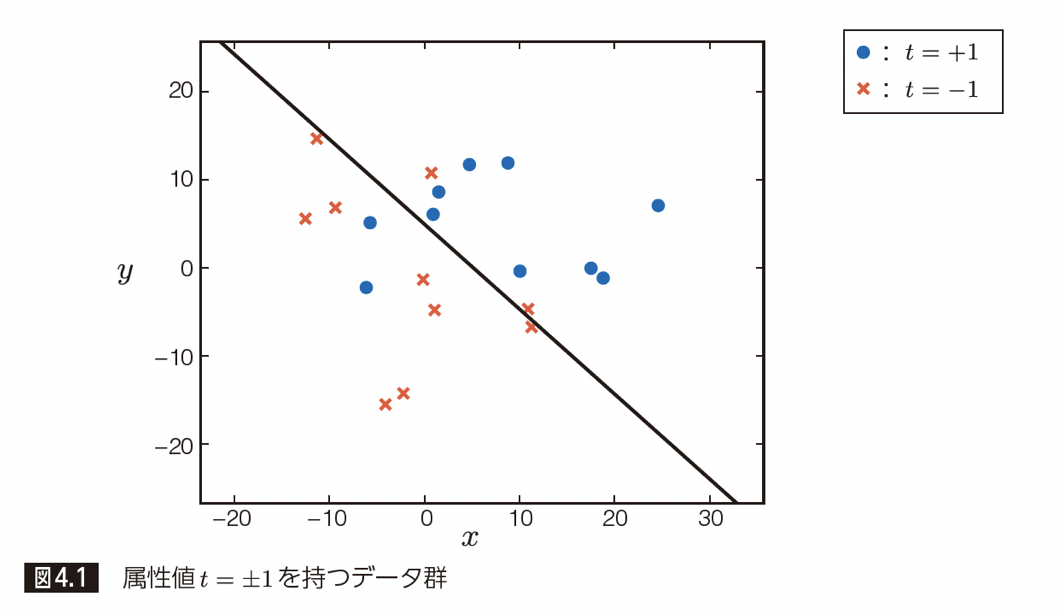
【平面にて直線で分類するイメージ】
そういった線形分類器の中でも、パーセプトロンは分類アルゴリズムの基礎ともいえます。直接本書では触れられていませんが、ニューラルネットワークにも深く関わりがあります(本記事のコラム参照)。
このパーセプトロンアルゴリズムを解く流れは、 2 , 3 章と変わらず「パラメトリックモデルの 3 つのステップ」に従いますが、最後の「最良の評価を与えるパラメーターを決定する」ステップで数式を直接解くことが出来ない場面に出くわします。
パラメトリックモデルの 3 つのステップ:
- パラメーターを含むモデル(数式)を設定する
- パラメーターを評価する基準を定める
- 最良の評価を与えるパラメーターを決定する
本章では、こういった場合でも解(答え)を近似的に導く手法である「勾配降下法」についても詳しく説明します。
勾配降下法は、機械学習モデルのパラメータを決定するアルゴリズムとして基本となる手法であり、その名の通り傾き(勾配)を利用して徐々に解へ近づいていく(降下)手法です。
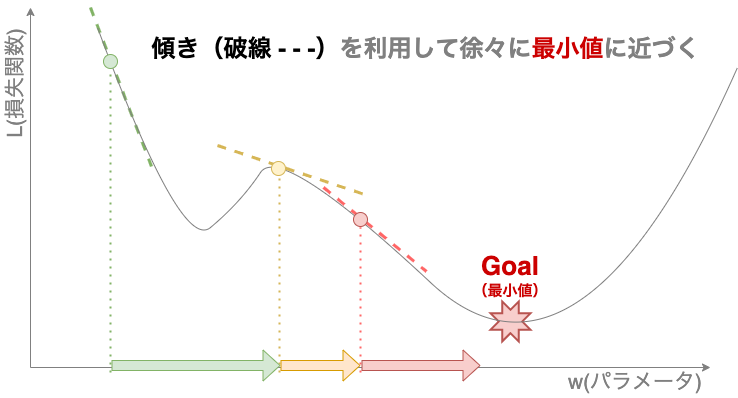
【勾配降下のイメージ】
2 , 3 章における最小二乗法,最尤推定法が「2 . パラメータを評価する基準を定める」ステップにおける基本となる理論だとすると、本章の勾配降下法は「3 . 最良のパラメーターを評価する基準を定める」ステップにおける基本となる理論といえます。
本記事では、以下の順で説明していきます。
- パーセプトロンの概要
- 機械学習におけるパラメータ決定の基礎:勾配降下法
本章は、序文で「機械学習らしいアルゴリズムの世界が始まります」と述べられており、機械学習を利用していく中でとても重要な理論を紹介しています。理解すれば、今日のニューラルネットワークを理解する第一歩にもなるでしょう。
また、先に述べましたが、パーセプトロンとニューラルネットワークの関係について補足としてコラムにまとめています。ご参照ください。
パーセプトロンの概要
パーセプトロンの導入
繰り返しになりますが、パーセプトロンは線形分類器の一種です。線形分類器の最もシンプルなイメージとしては、以下の様に、平面を直線で分割するという図になるでしょう。

【平面にて直線で分類するイメージ】
この図においては、直線より上と下という形でデータを分類しているわけです。
パーセプトロンは、この分類方法をもう一段抽象化し、直線の上下という単純な分割でなく、直線の値を基にルールで分割するアルゴリズムです。
先程の図もパーセプトロンの一種と捉えることができるので、これを使って詳しく説明していきます。まずは、数式でパーセプトロンを表現していきましょう。
直線は、以下のような 1 次関数で表せます。
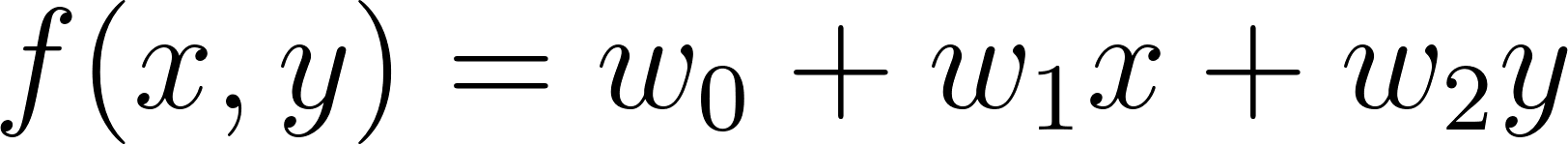
この直線で、t = ± 1 の 2 種類の属性を持つデータを分類しているとします。単純な上下での分類は、以下のような式で予測結果 t’ を算出しているといえます(ただし、直線上は t = -1 に含めるとします。)
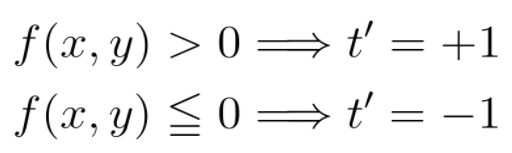
これは、
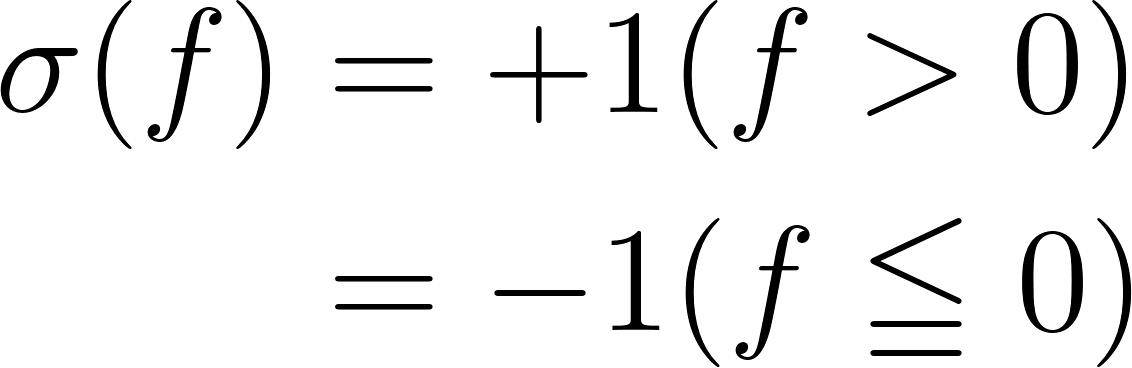
という関数 σ に f(x,y) の出力を入れたと考えることができます。
つまり、線形関数 f の結果を別の関数 σ にいれて、その結果 σ (f) で分類するのがパーセプトロンの一般化となります(この σ は活性化関数と呼ばれます)。入出力と関数の関係性をイメージにすると、以下の様になります。(計算のためにバイアス項と呼ばれる定数項を入れています。)
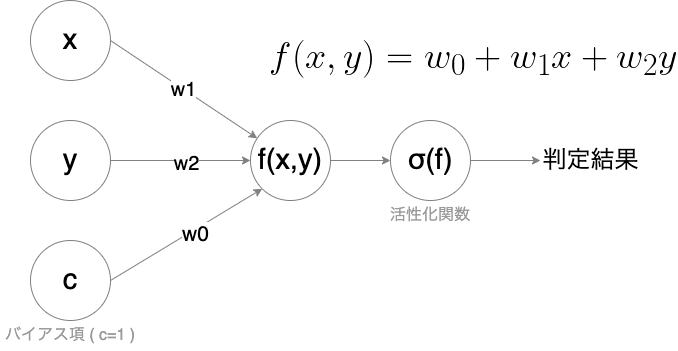
【パーセプトロンの入出力イメージ】
本書では、ここまでに説明したパーセプトロンの一種について解いていきます。
(本書における)パーセプトロンの解き方
実際に本書のパーセプトロンを解いていきましょう。
解き方の流れは、今までと同様に「パラメトリックモデルの 3 つのステップ」に従います。
- パラメーターを含むモデル(数式)を設定する
- パラメーターを評価する基準を定める
- 最良の評価を与えるパラメーターを決定する
1.パラメーターを含むモデル(数式)を設定する
まず、今回のアルゴリズムをモデル(数式)として定義しましょう。
パーセプトロンによってt=±1の2種類の属性が分類されます。
この予測結果の属性をt’とすると、予測結果 t ’は以下の 2 式によって分類されます。
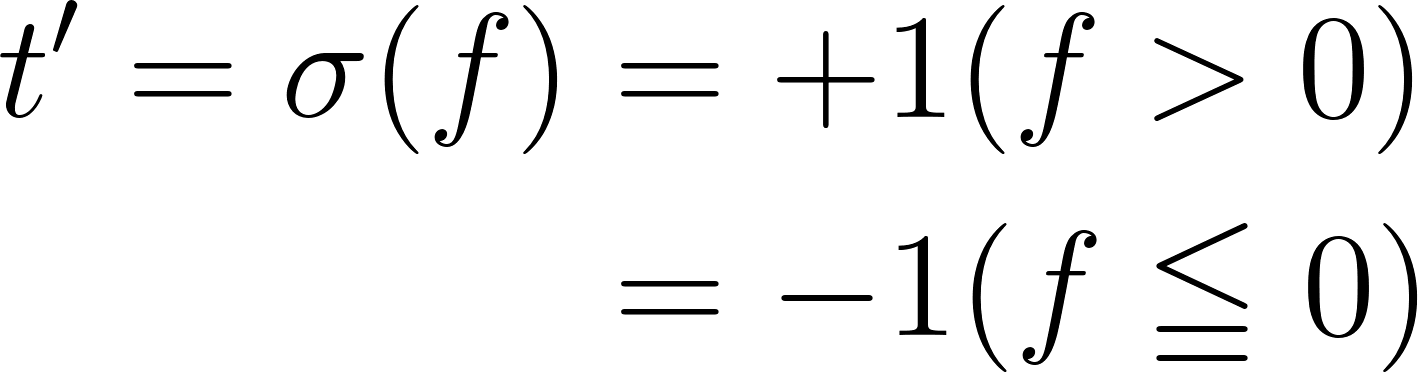
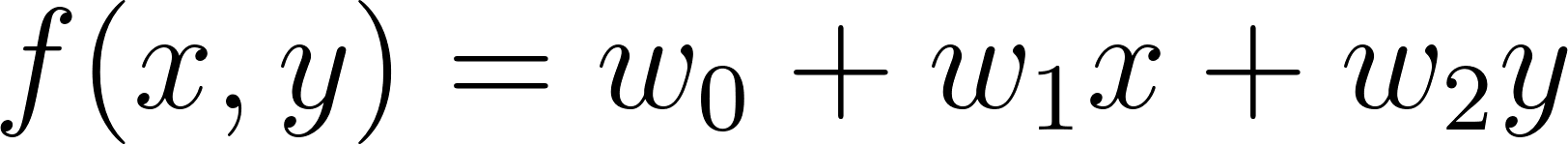
まとめて以下の様に表現することも可能です。
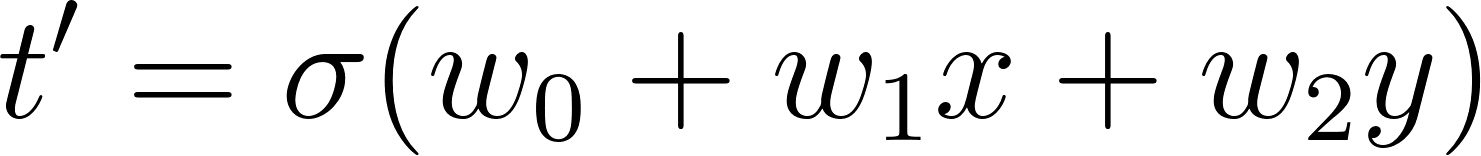
2.パラメーターを評価する基準を定める
モデルは定義し終えたので、パラメーターを評価する基準である、誤差関数を定義しましょう。
正しく分類されない場合、適切にペナルティを与えるような関数を定義する必要があります。
(回帰といえば最小二乗誤差と同様に、分類においてはコレといった誤差関数も存在します。しかし本書では、理解のため、あえて一から意味を考えて誤差関数を設計していきます。)
今回のケースであれば、正しく分類出来た場合、実際の属性 t とf (x,y) の符号が一致します(厳密にいうと、直線上の点はイコール0となるため一致しません)。
というのも、上式から以下のような関係が導けるからです。
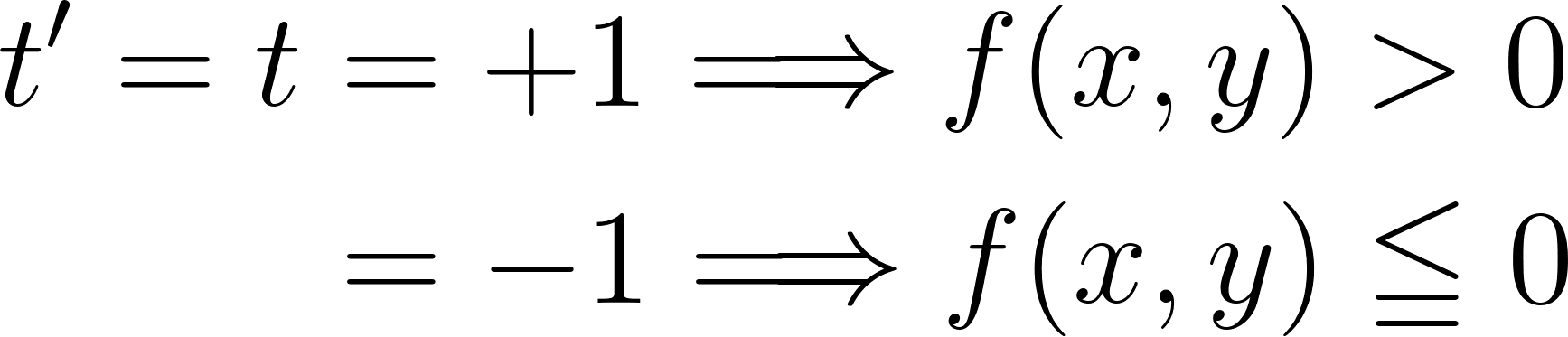
言い換えると、f (x,y) × t > 0 なら正しく分類できており、それ以外は間違っているわけです。
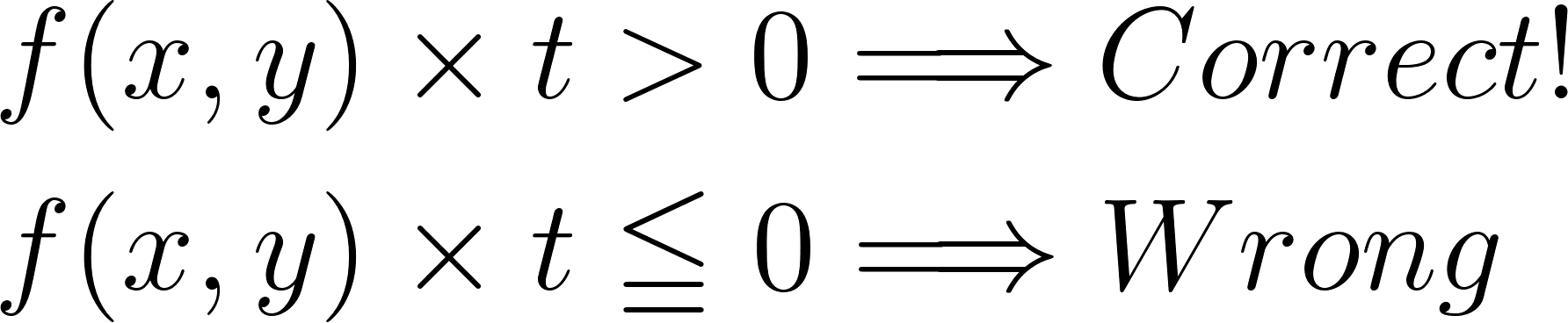
この式を利用して、間違ったデータ点 (x, y) を全て抜き出します。そして、それらの誤差を合計して誤差関数とします。
この誤差については、境界(赤い直線)から離れていればいるほど間違いが大きいと考え、f (x,y)の絶対値とします。
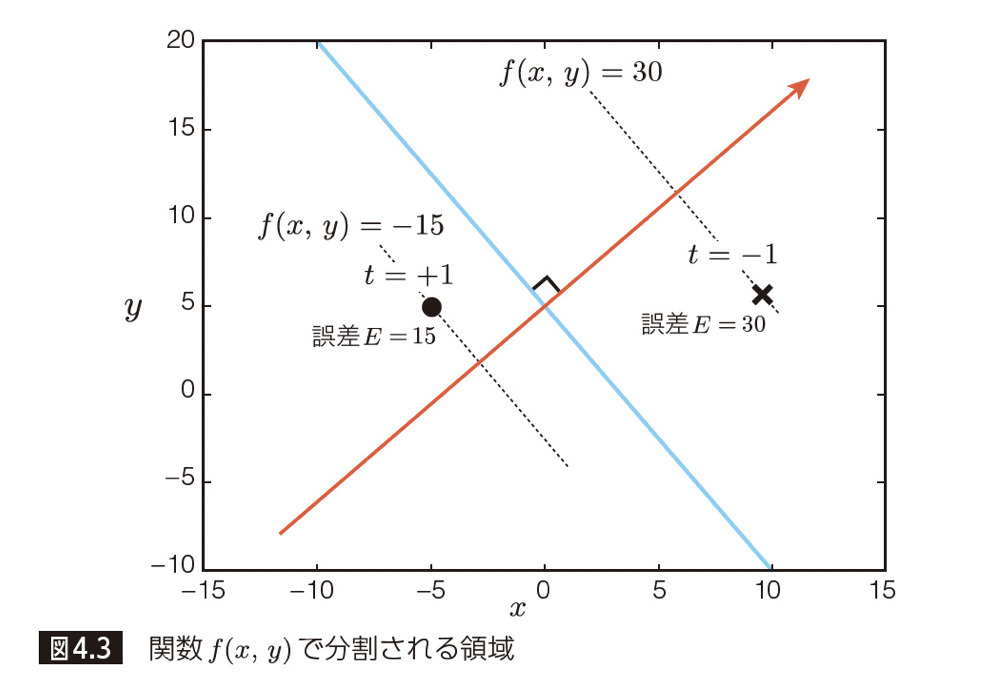
【平面における誤差のイメージ】
つまり誤差関数 E は、f (x,y) × t ≦ 0 を満たすデータ点(x_n, y_n)に対して誤差を合計した以下の式で表されます。
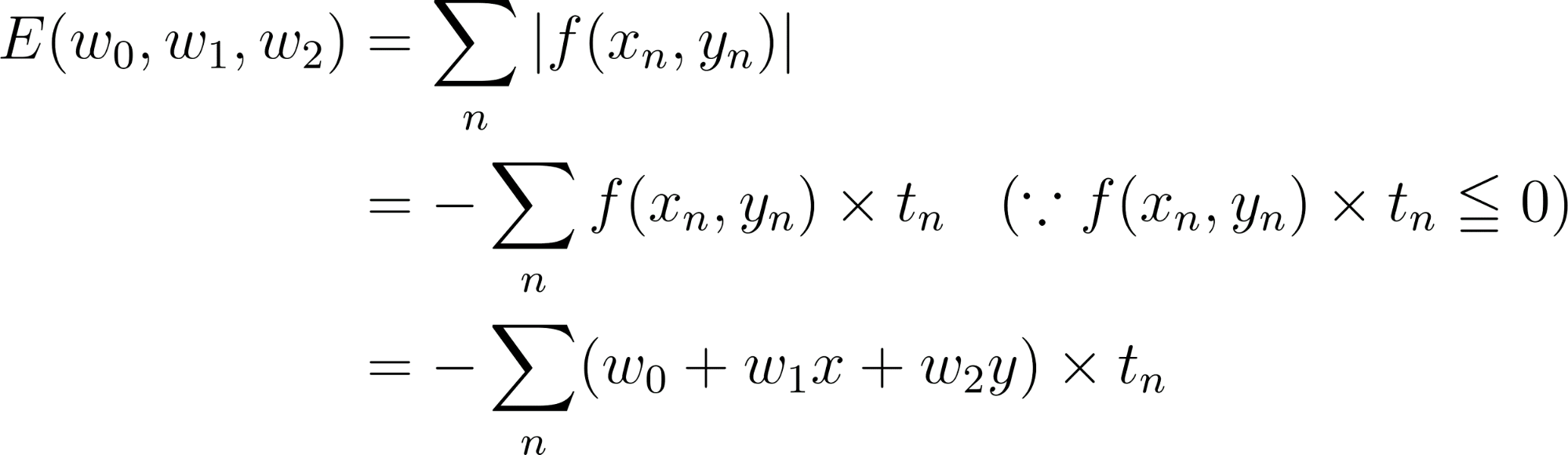
さて、この式 E を w の関数とみなして最小化します。最小二乗法の様に偏微分して E = 0 になるw を求めましょう!・・・無理です。
詳しい説明は本書を読んでほしいのですが、簡潔に言うと「誤差関数を求めるために利用するデータ点(x, y)が w の値によって変動し E の形が変わること」が原因になります。
データ点(x,y)が変わるたびに E が変化するのであれば、「wの値が変わるたびに E を定義しなおして計算する」ということを繰り返して E = 0 になる w を探して最適化するしかありません。この手法の一種が次に説明する勾配降下法になります。
機械学習におけるパラメータ決定の基礎:勾配降下法
勾配降下法の概要
勾配降下法とは、一言でいうと「式の傾き(微分)を利用して近似的に最小解を求める手法」です。
式の傾きを利用するとなぜ最小解を求められるかというと、数式が下に凸な場合、ゴールである最小値に行くためには、傾きを考えて進んで行けば良いからです。図のように、グラフの傾きをふまえて進む方向を、傾きの大きさをふまえて進む量を決めます。

【勾配降下法のイメージ】
よりイメージしやすいように現実に則した例をあげて説明します(この例は本書で書かれたものではありません)。
あなたが山で迷ったとします。なんの手がかりも無い時に、この山から麓に降りようと思った場合どうするでしょうか?
おそらく現在の位置より下へと降りていくのではないでしょうか。山がきれいな三角形であれば、時間はかかるかもしれませんが、いつかは麓に着くと思うでしょう(実際は、遭難したら動かないのが一番らしいですが・・・)。
さて、傾きを利用して解く勾配降下法のイメージがついたところで、今までの数式を解く手法と比べたときのメリットを述べます。メリットは大きく 2 つになります。
勾配降下法のメリット 1
1 つ目は先程述べた通り、解くことができない方程式の解を近似的に出すことができることです(先程までの解くことができる方程式を正規方程式と言ったりします、つまり言い換えると正規方程式でない方程式の解を出せると言ってもよいでしょう)。
勾配降下法のメリット 2
2 つ目は、訓練データの一部で訓練を進める事が出来るということです。(理論を説明するという趣旨の本書では取り上げられていませんが、実際の利用においては重要な場面もあるので、本記事では念の為ご紹介します。)全データをつかう勾配降下法と比較して、一部のデータを利用して勾配を計算する勾配降下法を「バッチ勾配降下法」と呼ぶこともあります。バッチ勾配降下法は、全データをメモリに収める必要がなく、要求するマシンスペックのコスト削減、計算コストの削減による訓練の高速化を見込めます。
これは、先程の例を用いると視界に入った地形を用いて降りる方向を判断することに似ています(四方の地形をある程度散策した上で決める人もいるかもしれません)。つまり、山の地形の一部を使って傾きを予測しているわけです。
勾配降下法の注意点
いいこと尽くめのような勾配降下法にも勿論デメリットが存在します。それは「解が収束しない可能性がある」ということです。つまり、答えに到達出来るとは限らないのです。迷い続けて永遠に麓につけないという状況が起き得ます。
この原因は大きく以下の 2 つです。
- 学習率の設定が悪い
- 勾配計算に利用しているデータのサンプリングが悪い
これらを、それぞれ例で言い換えると、
- 一度に進むと決めた距離の設定が悪い
- 下る方向の判断に利用した周囲の地形が特殊だった、地形への観察が足りなかった
と言い換えられるでしょう。詳しく説明します。
学習率の設定が悪い(一度に進むと決めた距離の設定が悪い)
まず、学習率ですが、これは傾きに対してどれぐらい進むかを決定するハイパーパラメーター(人の手で決定するパラメーター)になります。これが大きすぎると、解を飛び越えることを繰り返し、永遠に答え(最小値)へたどり着きません。
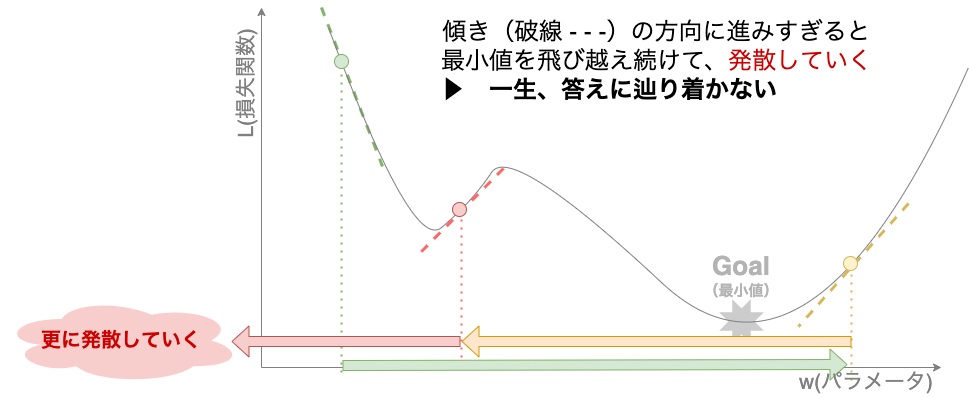
【学習率が大きい場合のイメージ】
かと言って小さすぎても訓練が遅くなります。最悪なのは、最小地点でないけれど周りより小さい地点(局所最適解)に捕まった場合です。あらゆる関数がきれいに山なりだとは限りません。凸凹している可能性もあります。この場合、一生抜け出すことができません。(先程の例で言えば、山脈から麓へ抜け出す際に谷に到達してしまったような場合です。)
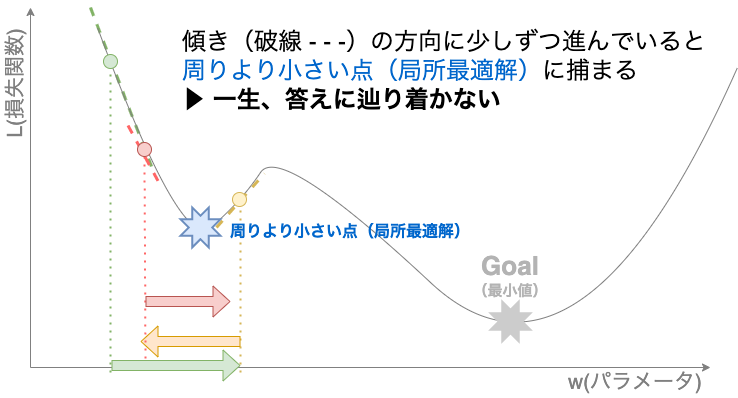
【学習率が小さい場合のイメージ】
つまり、学習率は、高すぎず低すぎず丁度よい値を選ぶ必要があります。この選び方については、それだけで一つ本が書けてしまうぐらいの情報量があるので、この本では触れられていません。気になる方は是非調べてみてください。
勾配計算に利用しているデータのサンプリングが悪い(下る方向の判断に利用した周囲の地形が特殊だった、地形への観察が足りなかった)
次にデータサンプリングについてです。これは、全データを利用しない勾配降下法のみの話ですが、全データを利用する勾配降下法よりも使う頻度が高いので詳しく説明します。
サンプリングの問題は2つの要素へ分解できます。すなわちサンプリングしたデータの「質」と「量」です。
まず、簡単な方である「質」から説明します。これは「勾配計算において利用するデータが全データを代表したデータかどうか(分布の偏った部分からサンプリングされていないか)」ということです。サンプルが偏った結果、似たようなデータで誤差関数の勾配を計算すると、全てのデータに適合する適切な勾配が計算できません。よって、出来る限り均等にデータをサンプリングする必要があります。
ここでサンプリング時に、ランダム(確率的)にデータを取得するという手法を取れば上記の問題を和らげることができます。これは、今日のデフォルトとも言える確率的勾配降下法という手法になります。(確率的勾配降下法は、局所最適解に捕まっても抜け出す可能性があるというメリットもあります。)
次に「量」の話です。これは直接本書で取り上げられていませんので、本記事では触れるだけにしておきます。
要は「勾配計算時にどれくらいのデータを用いるか」( = 「バッチ数」とも言われます)という話ですが、結論をいうと大きくするか小さくするかは諸説あり、問題設定ごとに自分で決める必要があります。さらには学習率の値とも関連があるとも言われており、まさに機械学習の「職人芸」に相当する部分です。
まとめると、「勾配降下法を利用する際は確率的勾配降下法がデフォルトとなるが、学習率・バッチ数には注意を払って学習する必要ある」ということです。
これらを踏まえて、実際に解く過程を見ていきましょう。
勾配降下法で分類を解いてみる
本書ではシンプルに、
- サンプリングは順に一個ずつ
- 学習率は一定
という条件で、全ての点を正しく分類出来るまで訓練を行っています。(逆に、全ての点が正しく分類出来るという問題設定だからこそ、この条件で訓練して確実に解を収束させられるとも言えます。)
まず、先程の誤差関数 E の式に対して、重みとデータ点をベクトルとして表現します。ベクトル化すると、多変量でも対応出来るように一般化されます。
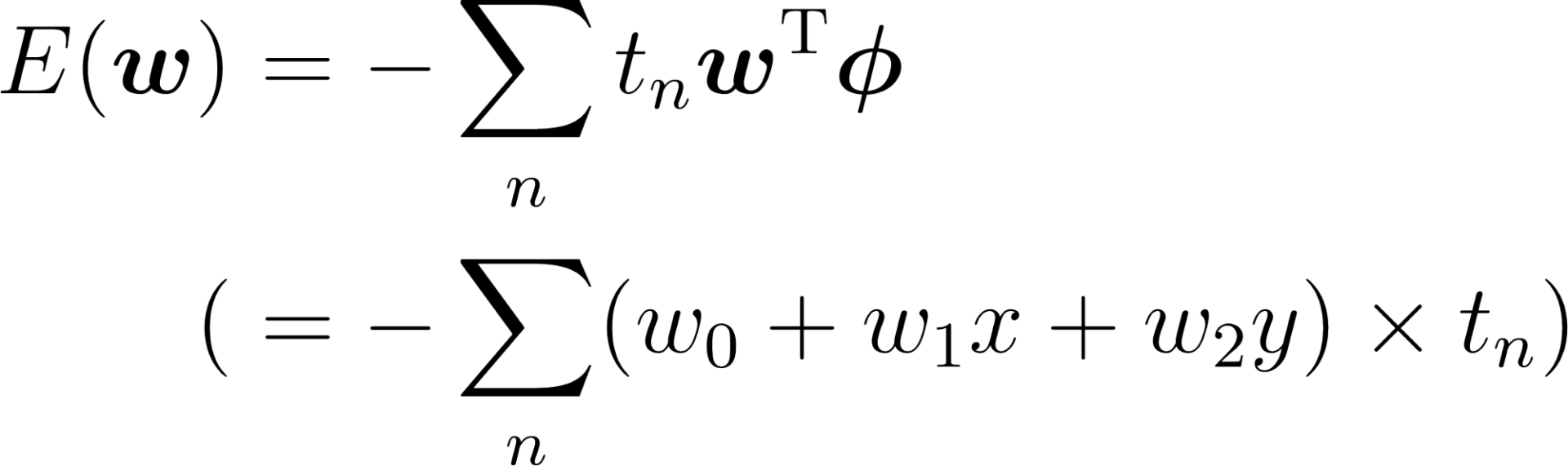
重みベクトル w :
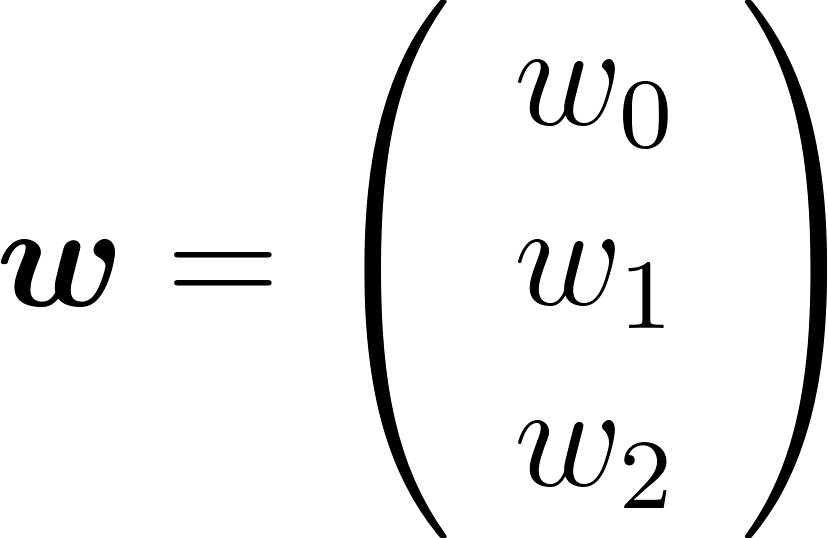
データ点ベクトル Φ:
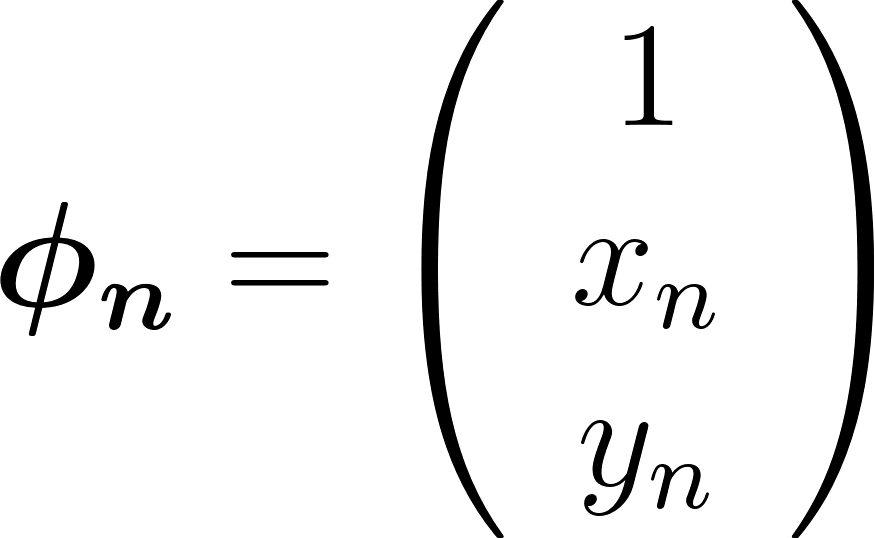
(計算の都合上、第一成分に定数 1 を入れています。これはバイアス項と呼ばれます)
後は、E の傾き ∇E を利用して w を更新していきます。∇(ナブラ)は傾きを取る記号です。傾きの方向とは逆に更新していけば解に辿りつくということは、数学的には「傾きを引く」という計算に相当します。(下図では傾きが負のため、正の方向にパラメータ w を更新しています。)
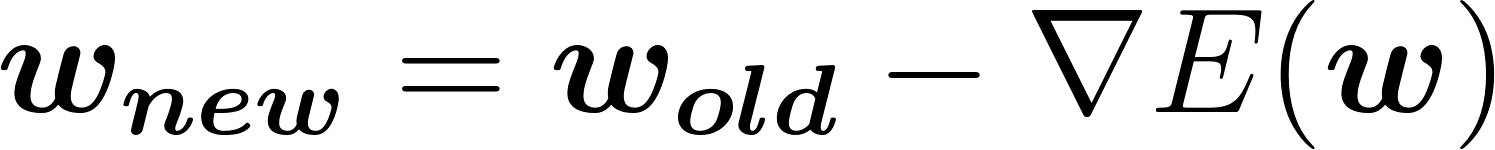
あとは、これをひたすら繰り返します。本書は訓練コードが実際に公開されているので、気になる方は是非試して見てください。
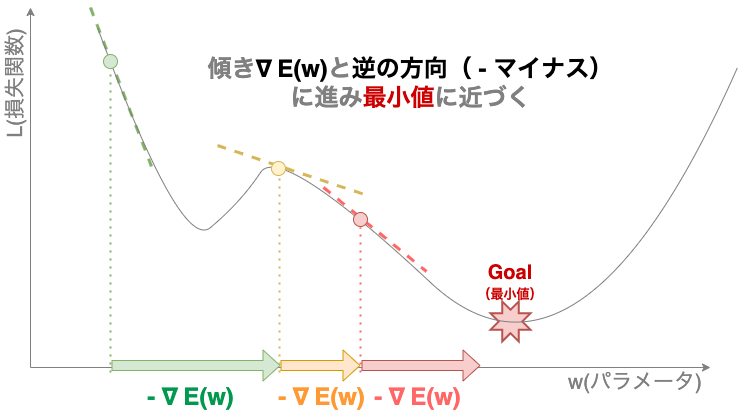
【勾配降下法の数式イメージ】
補足ですが、学習率 η を導入する場合は、上記の式が以下のように変形します。
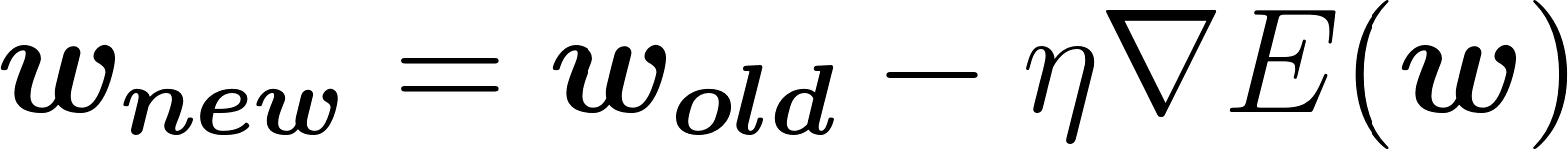
まとめ
本章は、2 , 3 章と変わり、分類アルゴリズムを題材にして話が進んでいきました。今までの回帰と問題を解く流れは同じでしたが、パラメーターを決定する際に利用した「目的の方程式を数学的に計算して解く」方法とは異なり、「目的の方程式を傾きを利用して近似的に解く」勾配降下法を新しく紹介しました。この勾配降下法は、機械学習モデルのパラメータ決定において極めて重要な理論であり、分類だけでなく回帰でも利用されます。
勾配降下法を用いたパラメータ決定において、学習率・バッチ数というハイパーパラメータが存在します。これらのハイパーパラメータはモデルの性能を大きく左右することもありますが、調整する際には本記事で紹介した理論を最低限理解している必要があります。
実際に取り上げたモデルであるパーセプトロンも重要なアルゴリズムです。コラムで紹介しますが、パーセプトロンを理解するということは、ニューラルネットワークの基礎を理解するということと同義です。機械学習の理論を理解する第一歩として良いモデルと言えるでしょう。
また、誤差関数をゼロから作成しているのも、個人的には面白かった点です。今日はTensorFlowといったような機械学習ライブラリも充実しており、与えられた誤差関数を利用することがどうしても多くなります。しかし、式を見て意味を考えることで、この誤差関数が設計された理由を洞察出来るのだと感じました。
本書では、以下のような観点からも理論を掘り下げています。
- パーセプトロンの幾何学的意味
- バイアス項について
もし、興味がある方は、是非手にとって確認してみましょう。
コラム: パーセプトロンとニューラルネットワークの関係
パーセプトロンは、線形結合の結果を活性化関数にいれるというシンプルなモデルでした。実は、このシンプルなモデルでは解けない問題が存在します。(例えば、解けない問題として排他的論理和の分割が存在しますが、ここでは詳細を割愛します。)
しかし、パーセプトロンを積み重ねることでこれらは解決します。層を重ねることで、モデルは複雑性を増し、解ける問題の幅も広がるのです。
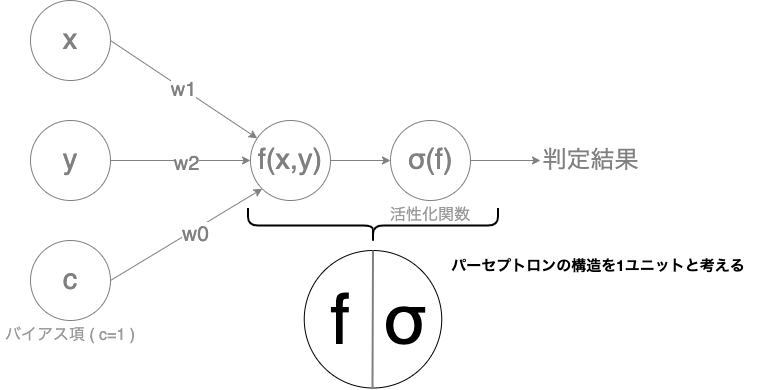
【パーセプトロンのイメージ(復習)】
このモデルは、マルチレイヤー・パーセプトロン(MLP)と呼ばれます。パーセプトロンを複数並列化して層とし、前の層の出力が次の層の入力になるということを繰り返したモデルです。
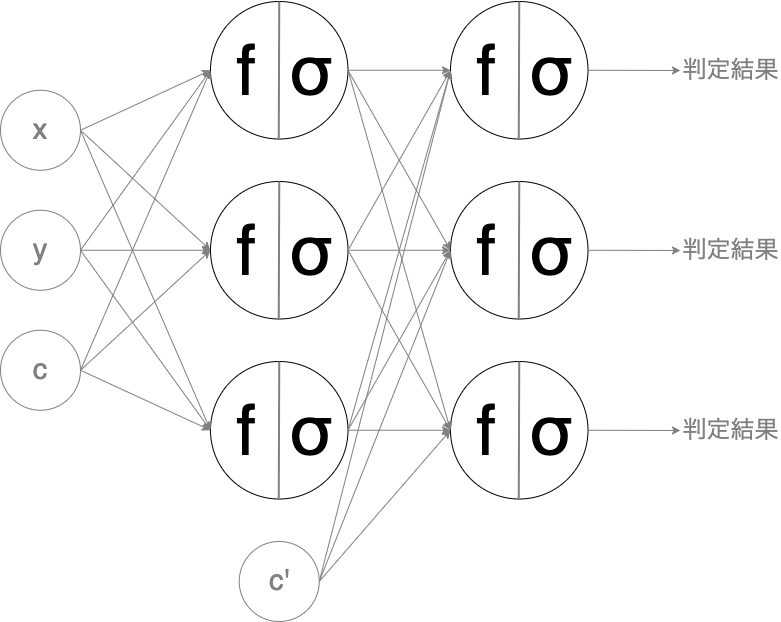
【MLP の一例(層やユニットは可変)】
見たことがある図だと感じた人もいるかも知れません。この図は、単純なニューラルネットワークにそっくりです。なぜならば MLP こそがニューラルネットワークの原型だからです。
ここから以下のような理論的な革新を経て、今日の様々なニューラルネットワークに発展しました。
- 多層の勾配を効率よく計算する方法
- 活性化関数の最適化
- 単なる全結合ではなく複雑なアーキテクチャ
発展を支えたのは理論的側面だけではありません。層が深くアーキテクチャが複雑になり、データも膨大になれば、要求されるハードウェアも強力なものが必要となります。
ハードウェアの発展も著しかったことがニューラルネットワークの発展を支えたのです。ハードディスクは指数関数的に安くなり、コンピューティング能力も指数関数的に上昇しました。
こういった強力なハードウェアの力を手軽に借りることが出来るのがクラウド・コンピューティングです。現代においては、クラウドがあるからこそビジネスレベルで機械学習が活用出来るようになったと言っても過言ではないでしょう。
本書や本記事を読み、ビジネス利用をしたいと考えた方は、是非 Google Cloud™ で機械学習を試してみてください!!!
次の第 5 章では分類アルゴリズムに最尤推定法を組み合わせた手法である「ロジスティック回帰」と分類アルゴリズムの評価手法である「ROC 曲線」が登場します。
※ Google Cloud は、Google LLC の商標です。
※ この記事は、本書籍で扱われているトピックについて、クラウドエースのメンバーが独自の見解で補足説明を加えたものになります。
| 章 | タイトル | 概要 |
|---|---|---|
| 1 | データサイエンスと機械学習 | ビジネスにおけるデータサイエンスの役割とデータサイエンスと機械学習の関係性を学ぶ |
| 2 | 最小二乗法: 機械学習理論の第一歩 | 「最小二乗法」で回帰分析を行い、機械学習の理論的な基礎となる「統計モデル」と基本のワークフローを理解する |
| 3 | 最尤推定法: 確率を用いた推定理論 | 「最尤推定法」で回帰分析を行い、確率を用いたモデルの役割について学ぶ |
| 4 | パーセプトロン: 分類アルゴリズムの基礎 | 分類アルゴリズムの基礎となる「パーセプトロン」と数値的計算手法の基礎となる確率的勾配降下法を学ぶ |
| 5 | ロジスティック回帰と ROC 曲線: 分類アルゴリズムの評価方法 | 最尤推定法を用いた分類アルゴリズムである「ロジスティック回帰」と分類アルゴリズムの評価方法について学ぶ |
| 6 | k 平均法: 教師なし学習モデルの基礎 | 「k 平均法」を用いて教師なし学習のクラスタリングについて学ぶ |
| 7 | EM アルゴリズム: 最尤推定法による教師なし学習 | 最尤推定法を用いた教師なしクラスタリングの手法として「EM アルゴリズム」を学ぶ |
| 8 | ベイズ推定: データを元に「確信」を高める手法 | 「ベイズ推定」で回帰分析を行う手法を学ぶ。ベイズ推定と最尤推定の違いを理解し、パラメータを確率的に推定するということを理解する |
クラウドエースとは
クラウドエースは Google Cloud 専門のシステムインテグレーターです。
Google Cloud の最先端の機械学習環境の活用について、豊富な知見を持つエンジニアがご要望にあわせて最適な形で技術支援をいたします。機械学習テクノロジーをご検討の際は、一度お気軽にお問い合わせください。
こちらの無料資料では、Google Cloud とクラウドエースについてさらに詳しく記載していますので、ぜひ合わせて御覧ください。

