
ITエンジニアのための機械学習理論入門
第3章 最尤推定法: 確率を用いた推定理論
こんにちは。クラウドエースのエンジニアの神谷です。
この記事は、Google Cloud 中井悦司さんの著書「IT エンジニアのための機械学習理論入門」の内容を参考に、機械学習の裏にある数学的な理論をわかりやすく紹介していきます。

昨今では、機械学習という技術がますます一般化されていますが、その分触れる事が少なくなった理論部分が、中井さんの書籍ではとてもわかりやすく解説されています。ここでは特に重要と思われるポイントを、章ごとに記事としてまとめています。「このような内容をもっと詳しく勉強したい!」と感じた方は、これらの記事を参考にしながら、中井さんの書籍を読んでいただければ、より深く掘り下げて理解を深めることができるでしょう。
本章の位置づけ
第 3 章では、モデルに「確率」の考え方を導入した最尤推定法を取り上げ、この最尤推定法を使った回帰分析を行います。最尤推定法の背景にある考え方や、2 章で説明した最小二乗法との違いを理解することができます。
最初のセクションでは、最尤推定法とは何かを具体例を交えて説明しています。筆者の理解をベースとしたストーリー形式になっており、厳密な説明となってはいませんが、最尤推定法の雰囲気を掴んで頂く手助けになればと思っています。
次のセクションでは、機械学習モデルの定式化と解き方について、2 章でご紹介した「パラメトリックモデルの 3 つのステップ」に沿って説明しています。
最尤推定法とは
最尤推定法とはなにか?
最尤推定法とは、端的に言うと「観測されたデータからそれを生んだ母集団を最もよく説明できる分布」を求める手法です。具体的には、あるデータ X(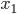
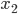
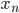
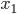
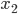
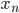
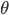
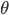
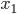
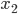
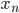
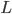
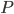
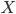
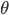
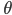
これだけだと分かりにくいと思いますので、例を出して説明します。(この例は本書で書かれたものではありません)。
まず、あなたはレストランを探していたとします。ちょうど良さそうなレストランがあったので、ここに入ることにしました。

そのレストランには「きまぐれ店長のおすすめコース」しかなく、店長のおすすめ料理が次々と出されるシステムでした。
最初に出てきたのは「タコライス」。美味しくいただきました。

次に出てきたのは「豆腐よう」。どこの料理だっけ?と思いつつも完食しました。

次に出てきたのは「ゴーヤーチャンプルー」。そこであなたは気づきます。「ああ、もしかしてここは沖縄料理屋ではないか」と。

ここで、あなたは次にどんな料理が出てくると思いますか?
ここまで来て次に「スパゲティ」が出るとは思わないでしょう。スパゲティは沖縄料理屋に限らずどこのレストランでも出るため、「これまでの料理の流れ的に出てきそう」な料理ではないからです。

この例から最尤推定法の説明に戻ると、次々と出てきた料理 X から、このレストランが何を主に提供するお店でどういったメニューがあるか、つまりデータ X を生成させる確率分布のパラメータ θ(何を主に提供しているのか)が段々と明らかになっていきます。今回の場合は、θ = 沖縄料理 と推定するのが妥当でしょう。このプロセスが「最尤推定法」です。
ここで、注意として「出てくる料理 X はもっとも発生しやすいものである」つまり「このお店は〇〇料理の定番を出してくる」という仮定を置きます。「タコライス」や「豆腐よう」、「ゴーヤーチャンプルー」は沖縄料理の定番なので、沖縄料理屋さんなのではないかと推定したので、この流れで「スパゲティ」が出てくるとは思わないでしょう。「沖縄料理屋」に入って出されるものは「沖縄料理」のはずであり、「スパゲティ」は「沖縄料理」を特徴づけるものではないからです。
ここまで 3 つの沖縄料理が出てきました。この流れから考えると 4 つ目の料理もきっと沖縄料理定番の「にんじんしりしり」あたりが出てくるのでは、と思うわけです。

最初にざっくりと設定した「次は〇〇料理が出てくるだろう」という仮定が、出てくる料理によって次第に状況がクリアになり、最終的には「次も沖縄料理が出てくるだろう」という結論に至ったわけです。まとめると以下のようになります。
- 確率分布 N(X | θ) → N :レストラン、X:出てきた料理、θ :沖縄料理屋
- 尤度 L = P (X | θ) → L :沖縄料理屋 θ から料理群 X が出てくる確率
- 尤度 L を最大化するように、出てきた料理群 X から逆にパラメータ θ を推定する(出てきた料理が増えるごとに、θ の値が「沖縄料理屋」に近づいていく)
なお、この例では、推定に用いるデータ(出てきた料理)が徐々に増えていくという流れで説明しましたが、実際に最尤推定を行う際は、すべてのデータが手に入った(すべての料理が出終わった)段階で、最終的な θ の推定を行います。すなわち、すべてのデータを使って計算した尤度 L を最大にするような θ を決定します。
最尤推定法で回帰を解く
最尤推定法を回帰で使うことを考えた場合、データ全体の分布傾向に加えて、データに含まれる誤差を併せて推定します。
下図で示すと、観測点(青点)は、① 緑線で示すデータ全体の分布傾向と、② 緑線からのズレ=誤差を表す確率分布(図中の釣鐘状の山)を持っており、それら両方を求めていくのが回帰における最尤推定法です。
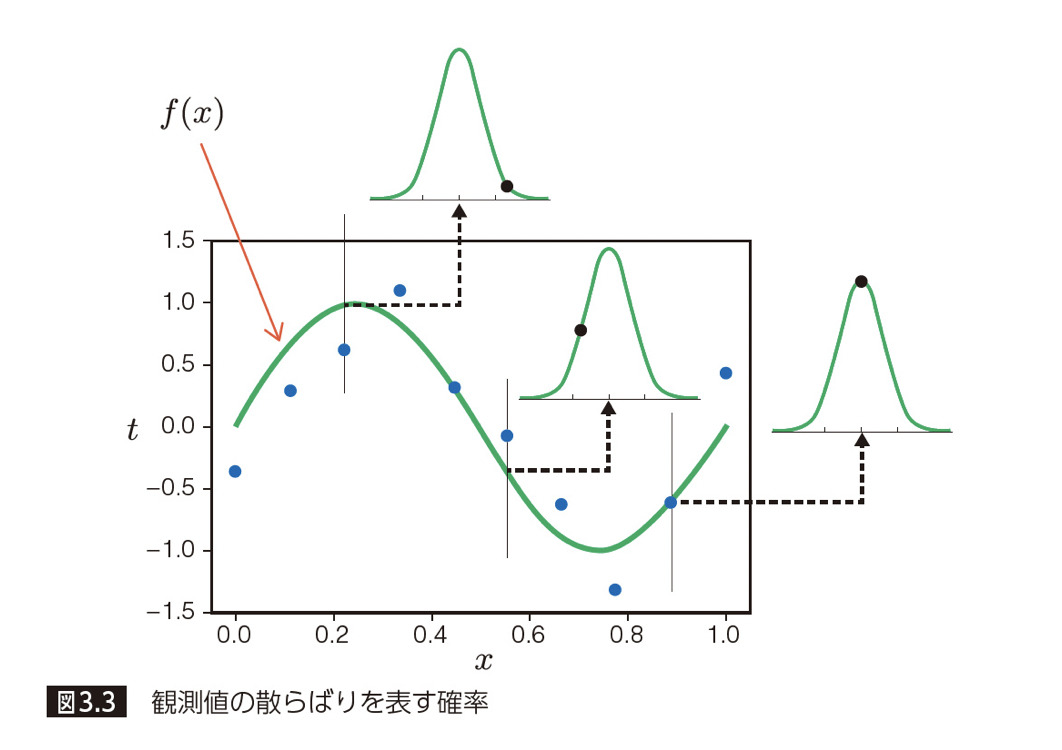
具体的な手順
以下に示す「パラメトリックモデルの 3 つのステップ」に沿って、最尤推定法で回帰を解いていきます。
(1)パラメーターを含むモデル(数式)を設定する
(2)パラメーターを評価する基準を定める
(3)最良の評価を与えるパラメーターを決定する
(1)パラメータを含むモデル(数式)を設定する
最尤推定では「データが発生する確率分布」を設定します。
ここでは、全ての観測点に対して、平均 u、分散 σ^2 の正規分布を仮定します。
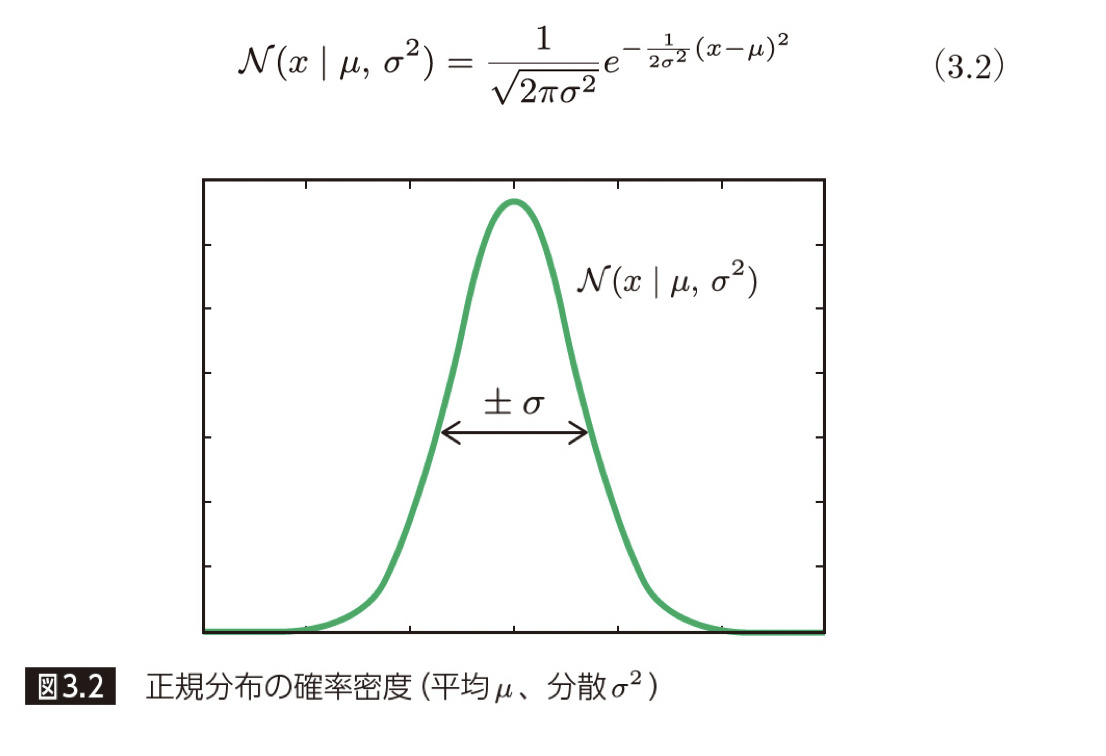
次に、「このデータの背後には M 次多項式の関係があり、さらに、標準偏差 σ の誤差が含まれている」という仮定を置きます(図 3.3 参照)。M 次多項式の関係を仮定するところは最小二乗法と同じですが、誤差についての仮定を追加した点が新しい部分になります。
このモデルを定式化すると以下のようになります。
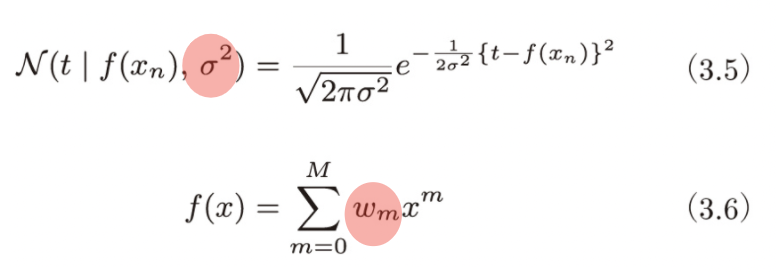
(3.5) 式が「データに含まれる誤差」、(3.6) 式が「データの背後にある関数関係」を表しています。詳細な数式証明は本書がわかりやすいのでそちらをご参照いただければと思いますが、最終的には上記の「σ(標準偏差)」と「w(M 次多項式のモデルの重み)」を求める問題に帰着します。
(2)パラメータを評価する基準を定める
ここでは先程出てきた (3.5) と (3.6) 式を使って、これらに含まれるパラメータを評価する基準を設定します。
(3.5) で t = tn を代入し、すべての観測点 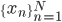
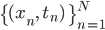
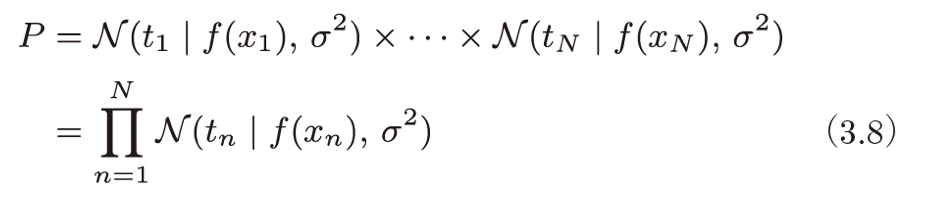
この確率はパラメータ(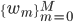
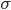
最尤推定では、上記の確率Pが最大になるようにパラメータを決定していきます。観測されたデータ(トレーニングセット)はもっとも発生確率が高いもの(最尤)であるとして、それらをかけ合わせた確率Pの最大化を行い、その時のパラメータを求めます。詳細な式変形は本書をご覧頂ければと思いますが、P は「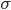
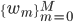
以下に公式として結果だけ掲載します。
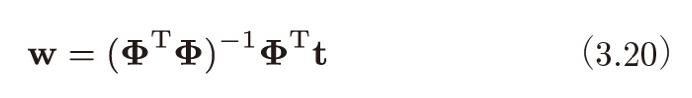
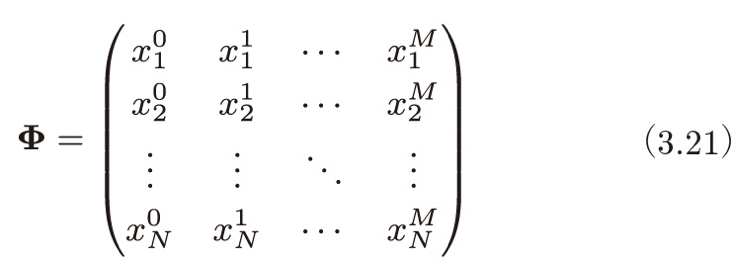
t はトレーニングセットの正解ラベルを並べたベクトルで、φ は N 個の観測点 x についてそれぞれを 0 〜 M 乗した値を並べた行列です。
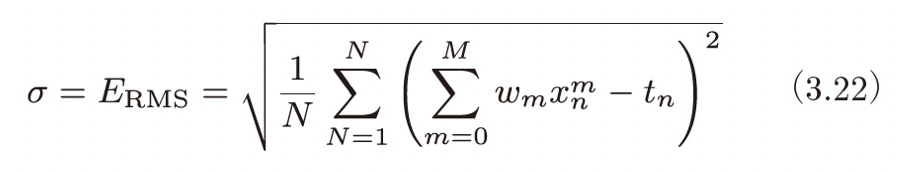
(3)最良の評価を与えるパラメータを決定する
「パラメトリックモデルの3つのステップ」の(1)と(2)ができたので、これをもとにデータセットを学習させて、最良の評価を与えるパラメータを決定(3)していきます。
下の図は、最尤推定法によって学習させたモデルに対して、「M 次多項式のモデルの重み」と、データの誤差である「標準偏差」を含めた推定結果を示しています。
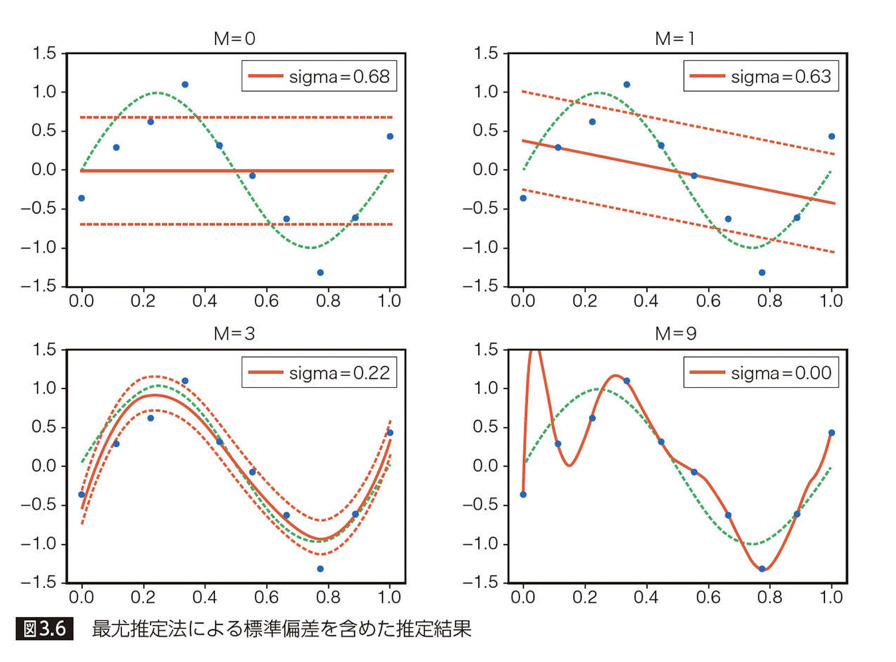
このグラフを見ると、多項式で予測される値とトレーニングセットに含まれる観測データの「ズレ」が、標準偏差(sigma)としてうまく表現されていることがわかります。多項式による予測値と実際の観測データの「平均的なズレ」である、平方根平均二乗誤差を標準偏差の推定値としているので、観測データは、標準偏差の範囲内にだいたい収まっています。
次数としては M = 3 の時に、あてはまりがよく、なおかつデータに適合しすぎない予測ができていることが分かります。
次は尤度と次数Mの関係について見ていきます。ここで、尤度に対して対数を取ったものが「対数尤度」と呼びます。トレーニングセットとテストセットに対して、次数Mに応じた「対数尤度」の変化は以下のようになります。
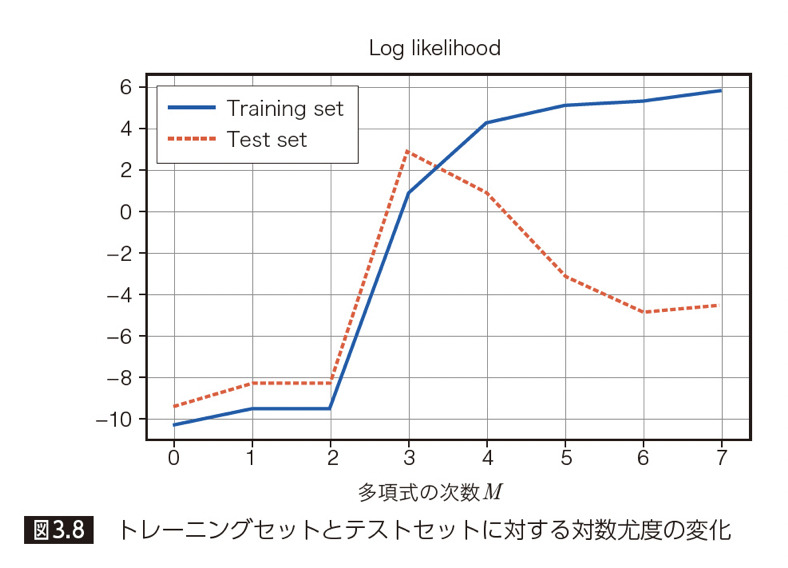
先程のパラメータ σ(標準偏差)のグラフからもわかったように、次数が M = 3 を境に、テストセットに対する尤度が低下していることが伺えます。ここで、トレーニングサンプル数N を 100 に増やした場合に、グラフがどのように変化するかを見てみましょう。
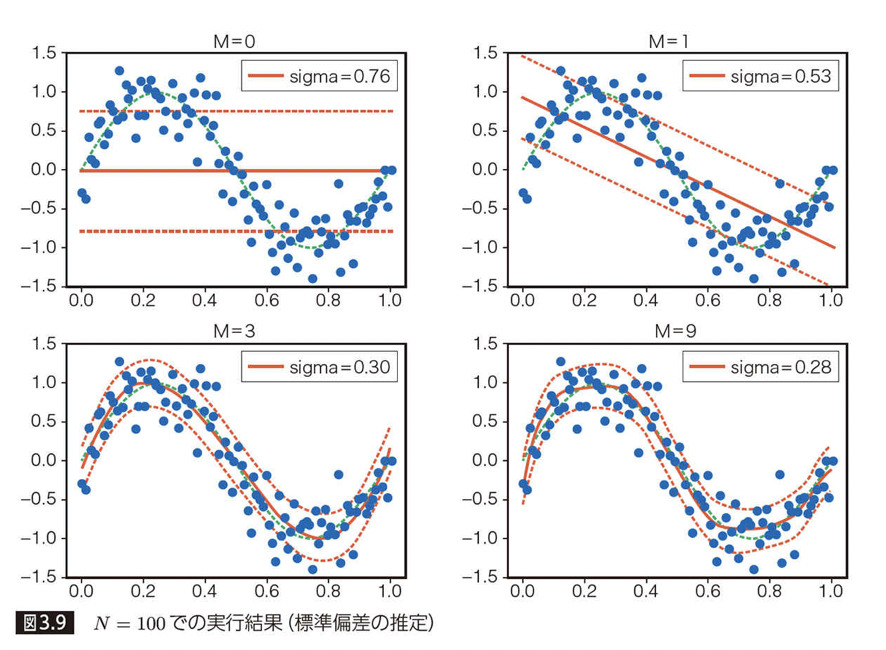
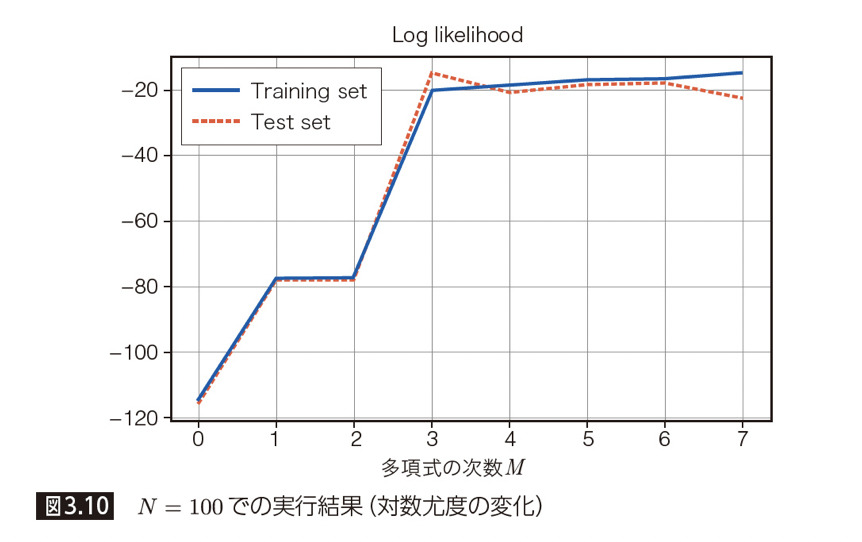
先ほどは M = 3 を境に性能が劣化していきましたが、トレーニングサンプルを増やしたことによって、パラメータ σ(標準偏差)と尤度 P のいずれにおいても性能が向上しています。このことから、より次数の大きい複雑なモデルにおいてもオーバーフィッティング(過学習)を起こさず、データを予測できるようになりました。
まとめ
今回の記事では、最尤推定法の概要や最小二乗法との違いについて説明しました。最尤推定法は「データが確率的に発生していること」を考慮した手法です。最小二乗法では「データの背後にある関数関係を推定する」ことが目的でしたが、最尤推定法では一歩進んで「データの背後にある関数関係に加えて、データに含まれる誤差を併せて推定する」ことがゴールになります。
次の第 4 章では基礎的な分類アルゴリズムである「パーセプトロン」が登場します。
参考リンク
※ Google Cloud は、Google LLC の商標です。
※ この記事は、本書籍で扱われているトピックについて、クラウドエースのメンバーが独自の見解で補足説明を加えたものになります。
| 章 | タイトル | 概要 |
|---|---|---|
| 1 | データサイエンスと機械学習 | ビジネスにおけるデータサイエンスの役割とデータサイエンスと機械学習の関係性を学ぶ |
| 2 | 最小二乗法: 機械学習理論の第一歩 | 「最小二乗法」で回帰分析を行い、機械学習の理論的な基礎となる「統計モデル」と基本のワークフローを理解する |
| 3 | 最尤推定法: 確率を用いた推定理論 | 「最尤推定法」で回帰分析を行い、確率を用いたモデルの役割について学ぶ |
| 4 | パーセプトロン: 分類アルゴリズムの基礎 | 分類アルゴリズムの基礎となる「パーセプトロン」と数値的計算手法の基礎となる確率的勾配降下法を学ぶ |
| 5 | ロジスティック回帰と ROC 曲線: 分類アルゴリズムの評価方法 | 最尤推定法を用いた分類アルゴリズムである「ロジスティック回帰」と分類アルゴリズムの評価方法について学ぶ |
| 6 | k 平均法: 教師なし学習モデルの基礎 | 「k 平均法」を用いて教師なし学習のクラスタリングについて学ぶ |
| 7 | EM アルゴリズム: 最尤推定法による教師なし学習 | 最尤推定法を用いた教師なしクラスタリングの手法として「EM アルゴリズム」を学ぶ |
| 8 | ベイズ推定: データを元に「確信」を高める手法 | 「ベイズ推定」で回帰分析を行う手法を学ぶ。ベイズ推定と最尤推定の違いを理解し、パラメータを確率的に推定するということを理解する |
クラウドエースとは
クラウドエースは Google Cloud 専門のシステムインテグレーターです。
Google Cloud の最先端の機械学習環境の活用について、豊富な知見を持つエンジニアがご要望にあわせて最適な形で技術支援をいたします。機械学習テクノロジーをご検討の際は、一度お気軽にお問い合わせください。
こちらの資料では、Google Cloud とクラウドエースについてさらに詳しく記載していますので、ぜひ合わせて御覧ください。

